Архив за месяц: Январь 2015

Обтекание цилиндра. Re=100…200

См. обтекание цилиндра при Re=1…30
Теперь рассмотрим обтекание цилиндра при Re=100…200, как известно в данном случае образуется вихревая дорожка Кармана при ламинарном течении. Т.е. для получения нужной картины вихрей необходимо использовать нестационарный метод. В данной статье выполним следующее:
1) Получим картину вихревой дорожки Кармана:
plot_XY_reedit
2) Определим изменение числа Струхаля от числа Рейнольдса (St=f(Re)) и сопоставим с эмпирической зависимостью;
3) Продолжим получение зависимости Cd=f(Re).
Особенность получения вихревой дорожки Кармана с помощью icoFoam – введение некоторой несимметричности. Иначе получится стационарный след, аналогичный вихрям Твина.

См. далее

Обтекание цилиндра. Re=1…30

Как известно, режим обтекания цилиндра зависит от числа Рейнольдса:
1) При Re=5…30 наблюдается образование вихрей Твина. Режим ламинарный, стационарный.
2) При Re=100…200 наблюдается вихревая дорожка Кармана. Режим ламинарный, нестационарный.
3) При Re>400 наблюдается вихревая дорожка Кармана. Режим турбулентный, нестационарный.

В данной статье рассмотрим п.1, ламинарное стационарное обтекание цилиндра диаметром d15 и числах Рейнольдса Re=1;5;15;30. Определим коэффициент полного сопротивления C_D и сравним с имеющимися опытными данными.
plot_XY
См. далее

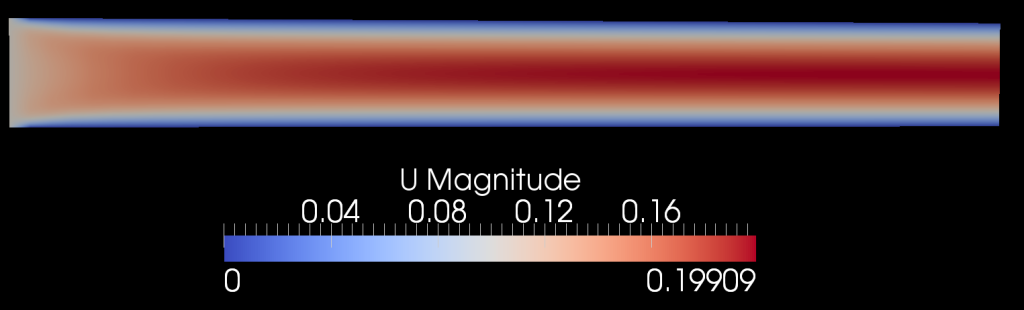
Стационарное ламинарное течение в трубе

В данной статье рассмотрю каким образом считается простейшее течение. В качестве примера возьмем течение на начальном участке трубы. Отсутствие необходимости определять турбулентные характеристики значительно упрощает задачу, т.к. решается обычное уравнение Навье-Стокса, без турбулентной вязкости или напряжений Рейнольдса:
\frac {dV} {dt} = F - \frac {1} {\rho} \nabla p + \nu \nabla ^2 V
где V – скорость потока, p – давление, F – массовые силы, t – время, \rho – плотность, \nu – молекулярная вязкость.
В статье сделаем следующее:
1) Сопоставим численное и аналитическое решение увеличения скорости на оси трубы;
2) Сопоставим параболический профиль с профилем скорости после смыкания пограничных слоев;
3) Сравним скорость расчета при использовании различных методов решения матриц.
plot_XY_tube_reedit
См. далее

Моделирование теплопроводности. Пример 3

Как я говорил ранее, граничные условия первого рода (фиксированная температура стенки) встречается на практике реже, чем условия третьего рода (через коэффициент теплоотдачи). В данной статье я покажу как использовать ГУ второго и третьего рода в openFoam при моделировании теплопроводности при использовании встроенных средств и сторонней библиотеки groovyBC.
Когда я впервые установил openFoam (была версия 1.8), встроенных средств для задания коэффициента теплоотдачи на поверхности не было, это можно было сделать только с помощью сторонней библиотеки groovyBC. Сейчас появилась возможность включать целые куски кода практически в любые места (ГУ, controlDict, blockMeshDict и пр.), что интересно с точки зрения освоения платформы, но на практике зачастую это удобней сделать все также через функции swak4foam. Встроенных граничных условий для задания коэффициента теплоотдачи все также нет.

Сначала я покажу на основе примера №1 возможности встраивания кода в 0/T. См. приложенный файл codedMixedLaplacianFoam.tar.gz. Найдем установившееся распределение температуры в бесконечной пластине (толщина 0,5 м, температуропроводность 1,33e-6 м.кв/с, теплопроводность 0,2 Вт/м*С) при задании граничных условий 3-го рода на одной стенке (температура охлаждающей среды -20 С, коэффициент теплоотдачи 10 Вт/(м.кв*С), и ГУ 2-го рода на другой (тепловой поток 200 Вт). Все значения специально подобраны, чтобы на одной стенке была температура 0 С, на второй 500 С.
См. далее

Моделирование теплопроводности. Пример 2

Проблемы примера №1 заключаются в следующем: 1) теплопроводность, теплоемкость и плотность материала зависят от температуры, 2) граничные условия 1-го рода редко встречаются на практике, чаще всего условия 3-го рода. В данном примере я покажу, как изменить стандартный солвер laplacianFoam для учета зависимости характеристик материала от температуры.
Решим задачу передачи теплоты теплопроводности через двухслойную бесконечную пластину толщиной 0,5 м, одна стенка которой нагрета до 800 С, вторая находится при 0 С.  Первый слой толщиной 0,25 м с температуропроводностью 1.33e-7 м.кв/с и коэффициентом увеличения теплопроводности b=0.0025 1/С. Второй слой толщиной также 0,25 м, температуропроводность 6,67e-7 м.кв/с, b=0,0006 1/C. Получим установившийся режим и сравним с ручным аналитическим расчетом.
См. далее

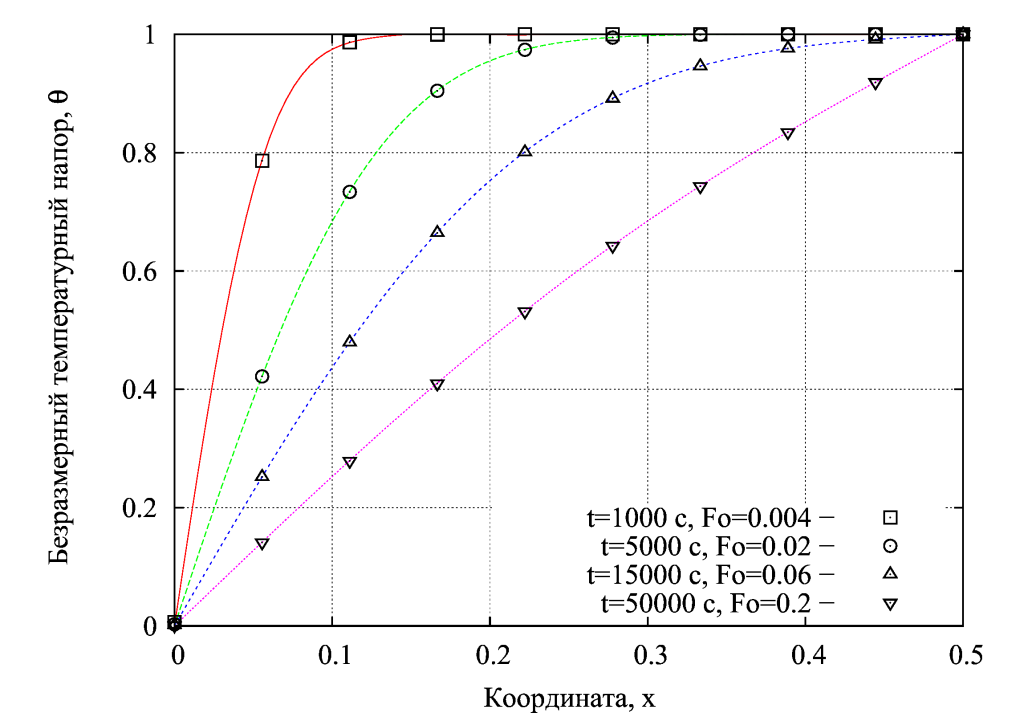
Моделирование теплопроводности. Пример 1.

Моделирование нестационарной теплопроводности – наиболее простая задача теплообмена, решаемая с помощью численных методов. Особенно это просто сделать при простой геометрии, постоянной теплопроводности и граничных условиях первого рода. В разнообраных вычислительных платформах это делается при минимуме необходимых настроек и соответственно трудозатрат. В данной статье рассмотрен расчет в OpenFOAM охлаждения неограниченной пластины с температуропроводностью 10^{-6} м.кв/с, толщиной 0,5 м, находящейся в начальный момент времени при t=500 c, если мгновенно уменьшить температуру одной стенки до t=0 С. Также выполнено сопоставление с аналитическим расчетом.

Дифференциальное уравнение распространения теплоты теплопроводностью при отсутствии внутренних источников достаточно простое [1]:
\frac {\partial T} {\partial \tau} = a \nabla ^2 T
где T – температура;
\tau – время;
a – температуропроводность;
\nabla ^2 – оператор Лапласа.
Код OpenFOAM в таком случае выглядит следующим образом [2]:

f(x)
См. далее