В данной статье рассмотрю каким образом считается простейшее течение. В качестве примера возьмем течение на начальном участке трубы. Отсутствие необходимости определять турбулентные характеристики значительно упрощает задачу, т.к. решается обычное уравнение Навье-Стокса, без турбулентной вязкости или напряжений Рейнольдса:
где V – скорость потока, p – давление, F – массовые силы, t – время, – плотность,
– молекулярная вязкость.
В статье сделаем следующее:
1) Сопоставим численное и аналитическое решение увеличения скорости на оси трубы;
2) Сопоставим параболический профиль с профилем скорости после смыкания пограничных слоев;
3) Сравним скорость расчета при использовании различных методов решения матриц.
Первая проблема, возникающая при моделировании любого течения, это сложность получения связанных полей скорости-давления. Поле давления является искомыми, при этом оно не выражено явно и находится из уравнения неразрывности (т.е если “правильное” поле давления подставить в уравнение Навье-Стокса, можно получить поле скоростей, удовлетворяющее уравнению неразрывности):
Решение следующее:
1) Предварительное задание поле давление p*;
2) Определение поля скоростей u*;
3) По данному полю скоростей вычисляется поправка к исходному полю давлений p';
4) Добавляем поправку давлений p’ к p*;
5) Расчет u по новому полю давлений;
6) Возвращаемся к п.2.
И так повторяем пока расхождение не будет меньше 1e-5. Сам метод SIMPLE хорошо изложен в переводе книги Патанкара [1].
Ламинарное течение в трубе характерно следующим:
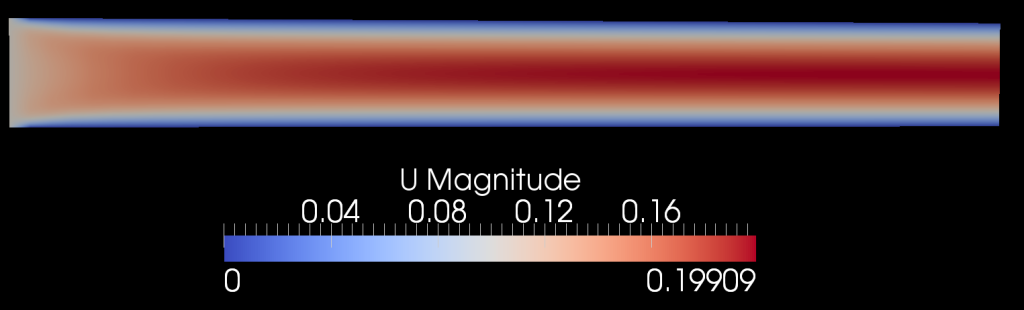
1) На начальном участке происходит образование пограничных слоев, которые “вытесняют” поток газа и происходит увеличение скорости на оси;
2) В установившемся режиме профиль – параболический, скорость на оси в 2 раза выше средней.
См. приложенный файл laminarTube.tar.gz
Примем следующую геометрию сетки: диаметр – 15 мм, длина – 140 мм. Принципиальная схема следующая:

Ниже приведена расчетная сетка, как видно к стенкам толщина ячеек уменьшается, для турбулентных течений необходимо соблюдать y+<1. Для ламинарных я нигде такого требования не нашел, но очевидно, что именно у стенок происходит наибольшее изменение скорости и именно там необходимо уменьшать размеры ячеек.
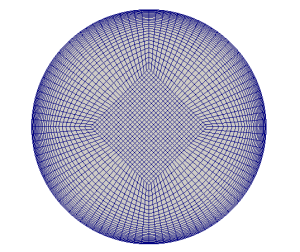

Для начальных граничных условий наверно пояснений не надо. На входе задаем фиксированное значение скорости и нулевой градиент давления, на выходе нулевой градиент скорости и фиксированное значение давление (в примере 0, но можно поставить например атмосферное, разницы нет), на стенках нулевая скорость и нулевой градиент давления.
Вообще simpleFoam используется для несжимаемых турбулентных течений, но его можно использовать и для ламинарных, для этого надо в constant/RASProperties указать
|
1 |
RASModel laminar |
и в constant/turbulenceProperties указываем
|
1 |
simulationType laminar |
.
Не смотря на то, что солвер стационарный указывать временной шаг все-равно надо, но он не несет никакой смысловой нагрузки, разве что названия папок, system/controlDict:
|
1 2 3 4 5 6 7 8 |
application simpleFoam; startFrom latestTime; startTime 0; stopAt endTime; endTime 1000; deltaT 1; writeControl runTime; writeInterval 1000; |
Решение сходится замечательно, поэтому можно не мелочиться и указывать самые точные схемы дискретизации дифференциальных уравнений в system/fvSchemes:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
ddtSchemes { default steadyState; } gradSchemes { default Gauss linear; } divSchemes { default none; div(phi,U) bounded Gauss linear; div((nuEff*dev(T(grad(U))))) Gauss linear; } |
Основные особенности заключаются в файле system/fvSolvers:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
solvers { p { // наилучший решатель матриц в данном случае solver GAMG; smoother GaussSeidel; // точность tolerance 1e-07; relTol 0.01; // изменить на 0 если не для давления используется nPreSweeps 1; // не меняем nPostSweeps 2; // не меняем cacheAgglomeration on; // не меняем agglomerator faceAreaPair; // экспериментально определено, что значение = sqrt(кол-во ячеек) nCellsInCoarsestLevel 500; // менять не надо mergeLevels 1; // ставим ограничение на количество итераций maxIter 100; } U { solver PBiCG; preconditioner DILU; tolerance 1e-8; relTol 0; } } SIMPLE { // сетка хорошая, сходимость тоже - значение 0, иначе увеличиваем nNonOrthogonalCorrectors 0; // решаем, пока значения не будут ниже следующих residualControl { p 1e-5; U 1e-5; } } // параметры релаксации, чем ближе к 0, тем меньше изменение между шагами relaxationFactors { fields { p 0.5; } equations { U 0.7; } } |
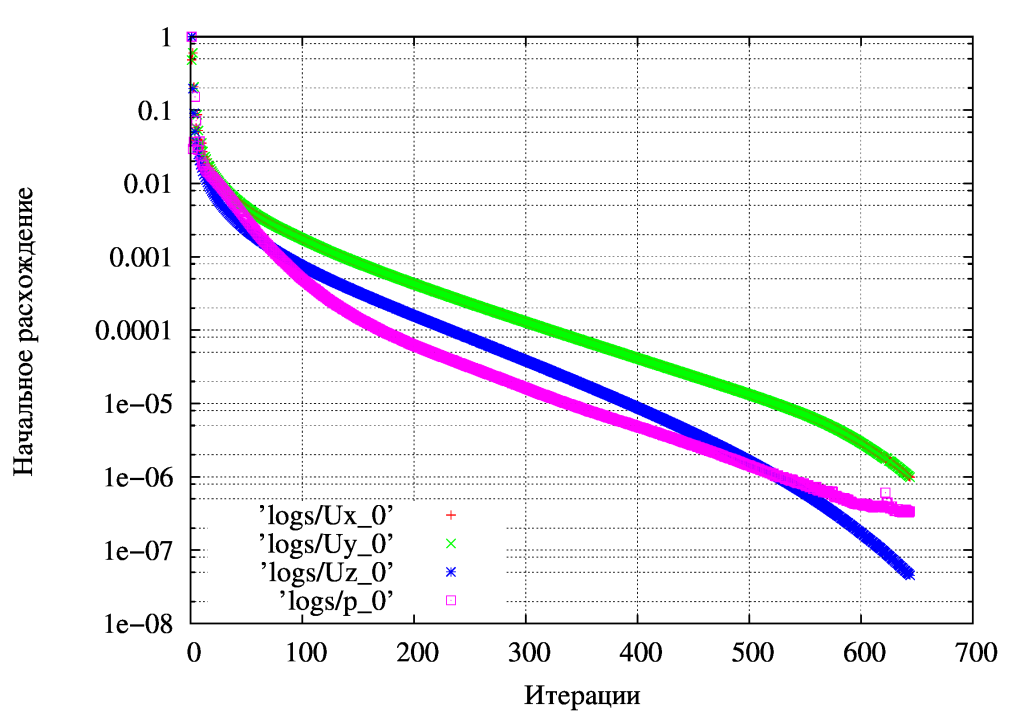
Решение сходится после 524 итераций, сделал небольшую серию, чтобы определить наилучшие параметры решения матриц
№ п/п Матрица p Матрица U Время
Опыт1 PCGDIC smoothSolver 982,89с
Опыт2 PCGDIC DILUPBiCG 947,25c
Опыт3 GAMG smoothSolver 626,46c //nCellsInCoarsestLevel 400;
Опыт4 GAMG DILUPBiCG 614,41c //nCellsInCoarsestLevel 400;
Опыт5 GAMG GAMG 702,29c //nCellsInCoarsestLevel 100;
Опыт6 GAMG GAMG 666,56c //nCellsInCoarsestLevel 250;
Опыт7 GAMG GAMG 617,04c //nCellsInCoarsestLevel 400;
Опыт8 GAMG GAMG 614,29c //nCellsInCoarsestLevel 550;
Видно, что опыты 4,8 самые быстрые (в примере аналогично опыту 4), их и рекомендую использовать.
Ниже приведен график сходимости до 1e-6 полученный через foamLog, видно монотонная сходимость, как и нужно:
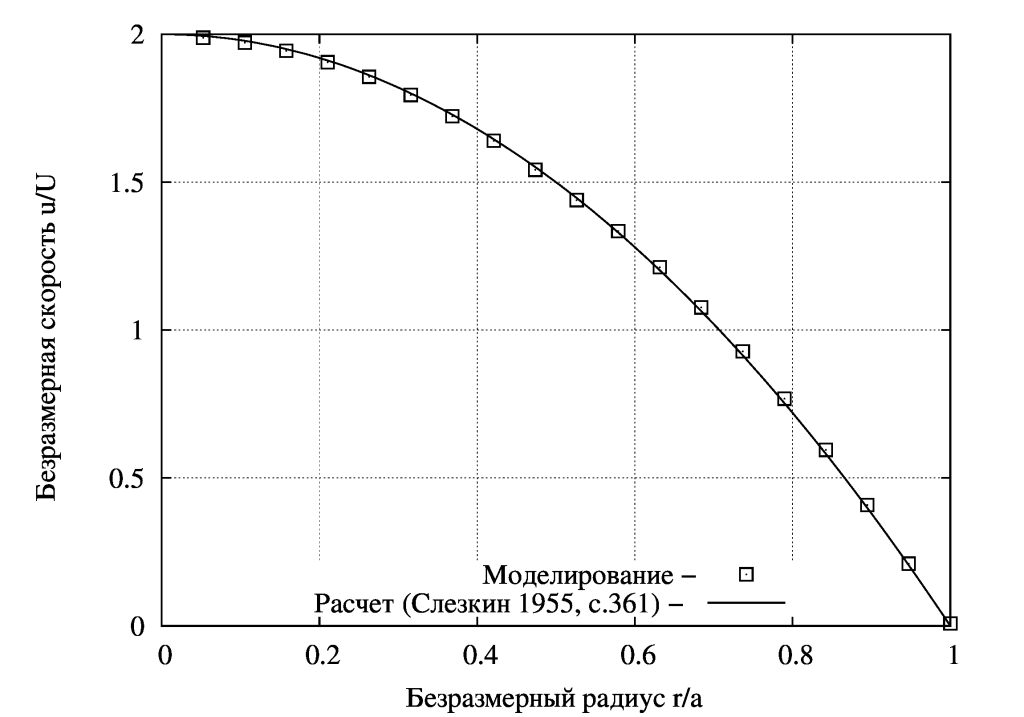
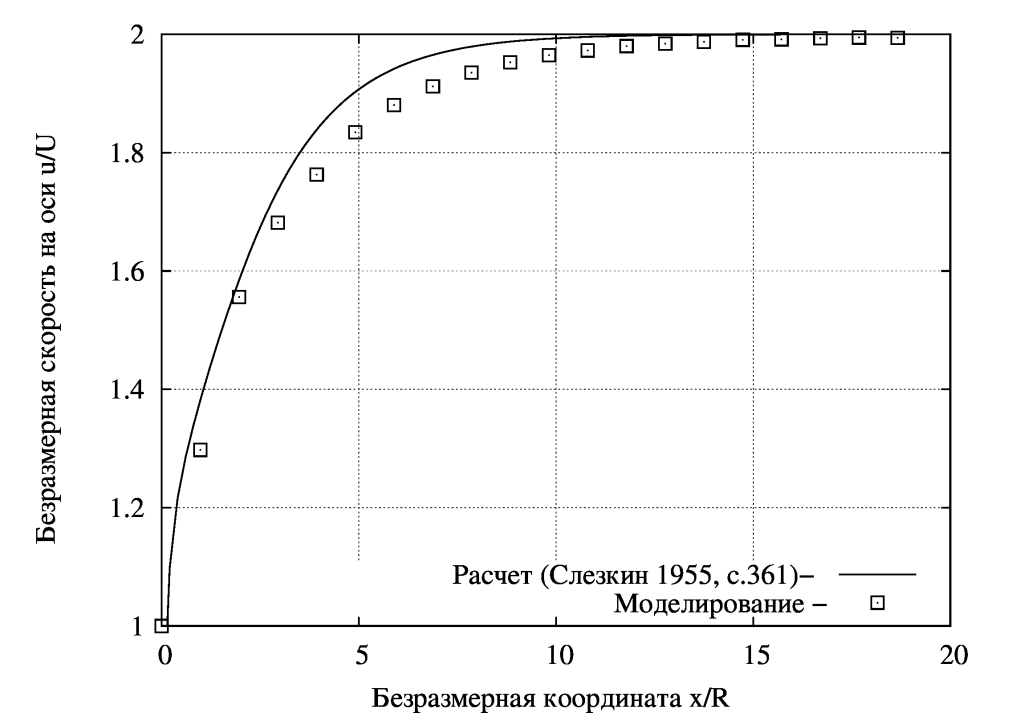
Профиль скорости снимаем по оси трубы и по радиусу в конце трубы:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
axis { type uniform; axis xyz; start (0 0 0); end (0 0 0.14); nPoints 20; } outlet { type uniform; axis xyz; start (0 0 0.14); end (0.0075 0 0.14); nPoints 20; } ); |
Сопоставим профиль скорости с параболическим:
Как видно сходится хорошо, а вот сопоставление изменения скорости по оси не очень, не известно из-за чего, быть может из-за допущений в аналитическом расчете [2]:

Литература:
1. Патанкар С. – Численные методы решения задач теплообмена и динамики жидкости, 1984 г. – М::Энергоатомиздат.
2. Слезкин Н.А, – Динамика вязкой жидкости. 1955 -М::Гос. изд-во.тех.-теор. лит-ры.