Именно с этой темы я и начинал знакомиться с openFoam-ом и численным моделированием. Задача оказалась абсолютно нетривиальной из-за сильно закрученного течения, образующегося в циклонном устройстве. На каждом форуме, посвященном ВГД, обязательно можно найти тему про данную задачу, например на cfd-online.com: 1, 2. Были и на форуме os-cfd.ru хорошие темы по моделированию циклонов, но форум куда-то пропал.

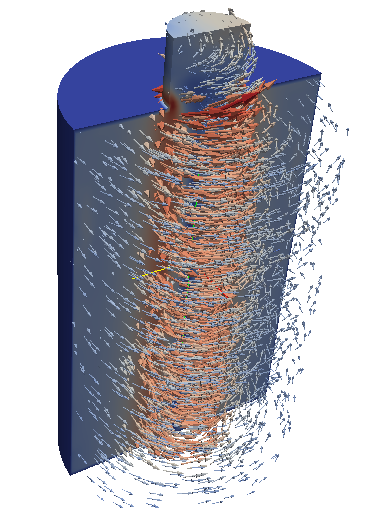
В данной статье я рассмотрю решение рассматриваемой задачи при использовании модели турбулентности Лаундера-Гибсона (LaunderGibsonRSTM);

В данной задаче есть две ключевые проблемы:
1) Одно- двухпараметрические модели (SA, k-Epsilon, k-Omega-SST) в оригинальной постановке не пригодны для моделирования закрученых течений, что приводит к завышению турбулентной вязкости и соответственно смещению максимума тангенциальной скорости к боковой поверхности. См. рисунки с cfd-online.com:

2) Подвод газа во внутренний объем ЦУ (циклонного устройства) выполняется тангенциально и очень сложно избежать вытянутых и скошенных ячеек, в области примыкания, см. рисунок ниже:

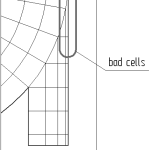
Я в итоге пришел к выводу, что оптимальный способ их избежать – убрать из геометрии и задать обычный параболический профиль прямо на боковой поверхности ЦУ:

Но данный способ не единственный и можно еще попробовать сделать следующее:
а) Неструктурированная сетка хорошего качества, но сделать ее с помощью snappyHexMesh сложно и требуется пляски с бубном;
б) Смещение тангенциальных входов ближе к оси, чтобы не образовывались вытянутые ячейки;
в) Можно создать структурированную сетку в виде “рулета”, это самый крутой способ, но также сложный (особенно если ЦУ требуется загружать какими-либо вставками).
3) Последняя проблема заключается в нестационарности самого процесса образования ядра течения (оно непрерывно колеблется, перестраивается и пр). При использовании simpleFoam и схем высокого порядка точности сошедшегося решения получить не получится. Можно попробовать использовать схемы первого порядка, но результат будет сложно предсказуемым.

Сетку для моделирования циклонных устройств я делаю через blockMesh и скрипты на bash-е, т.к. таким образом можно сделать удобную параметризацию геометрии (например, для изменения площади входов или диаметра выходного канала) и очень маленький размер файлов (удобно для дистационной работы, когда расчет производится не на домашнем компьютере, а расчитывается на каком-либо удаленном кластере). Из-за наличия осевого обратного течения, которое представляет собой газы, подсасываемые из окружающей среды через выходное отверстие, необходимо добавить к самому рабочему объему циклона еще и некоторый объем окружающей среды (выглядит как труба, поставленная на круглый выходной канал) для обеспечения однонаправленности потока и, соответственно, увеличения стабильности расчета.

Задачу решаем следующим образом (см. приложенный файл cycloneLaunderGibsonRSTM_v2.tar.gz:
1) Решатель – нестационарный, лучше pimpleFoam, можно pisoFoam. Расчет очень ресурсоемкий. Число Куранта, при котором относительно стабильно все считается 2.5 (pimple);
2) Конец расчета можно определить по давлению на боковой поверхности циклона, при развитии закрученного течения давление постепенно возрастает и потом становится постоянным. Поэтому целесообразно подключить runTime функцию по определению давления в точке на стенке;
3) После образования установившегося закрученного течения (см п.2) снимаем радиальные профили тангенциальной скорости за какой-нибудь отрезок времени (я обычно 0,3 с делаю) и осредняем скриптом на bash-е.
4) Параболический профиль по закону 1/7 можно задать через groovyBC. Зачастую на кластерах не удается его скомпилировать и можно использовать встроенные функции, для этого в 0/U пишем:

А в каталоге constant/boundaryData создаем папки inlet_1 и inlet_2 с файлами точек и значения скорости в них;
5) Граничные условия турбулентности (k epsilon R) находим по интенсивности турбулентности ~5% и характерному линейному масштабу – диаметру камеры. Все нужные формулы можно найти вот в этом Методическом пособии (где нашел не помню, автор не известен)
6) Для осреднения профилей скорости используем следующий скрипт:

Сопоставление расчетных и экспериментальных данных выполнено в нашей статье. Например, сопоставление безразмерных профилей тангенциальной скорости (dвых/Dк=0.2,0.3,0.4):

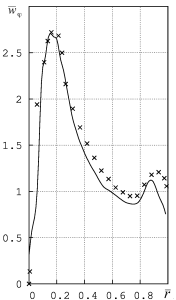
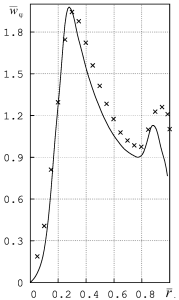
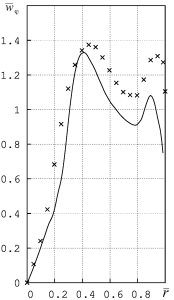
В целом, точность расчета незагруженных камер при использовании модели турбулентности Лаундера-Гибсона составляют: максимум тангенциальной скорости – 6%, радиус положения максимума тангенциальной скорости – 10,2%, коэффициент аэродинамического сопротивления – 14,9%, давление на боковой поверхности – 12,9%.