Моделирование теплопроводности. Пример 3

Как я говорил ранее, граничные условия первого рода (фиксированная температура стенки) встречается на практике реже, чем условия третьего рода (через коэффициент теплоотдачи). В данной статье я покажу как использовать ГУ второго и третьего рода в openFoam при моделировании теплопроводности при использовании встроенных средств и сторонней библиотеки groovyBC.
Когда я впервые установил openFoam (была версия 1.8), встроенных средств для задания коэффициента теплоотдачи на поверхности не было, это можно было сделать только с помощью сторонней библиотеки groovyBC. Сейчас появилась возможность включать целые куски кода практически в любые места (ГУ, controlDict, blockMeshDict и пр.), что интересно с точки зрения освоения платформы, но на практике зачастую это удобней сделать все также через функции swak4foam. Встроенных граничных условий для задания коэффициента теплоотдачи все также нет.

Сначала я покажу на основе примера №1 возможности встраивания кода в 0/T. См. приложенный файл codedMixedLaplacianFoam.tar.gz. Найдем установившееся распределение температуры в бесконечной пластине (толщина 0,5 м, температуропроводность 1,33e-6 м.кв/с, теплопроводность 0,2 Вт/м*С) при задании граничных условий 3-го рода на одной стенке (температура охлаждающей среды -20 С, коэффициент теплоотдачи 10 Вт/(м.кв*С), и ГУ 2-го рода на другой (тепловой поток 200 Вт). Все значения специально подобраны, чтобы на одной стенке была температура 0 С, на второй 500 С.

Проблем с заданием фиксированного теплового потока в принципе не возникает:

$q = -\lambda \nabla T$

т.е зная q и $\lambda$ задаем фиксированный градиент $\nabla T$ , все замечательно.

А вот с заданием коэффициента теплоотдачи все интересней.

$\alpha (T_0 - T_c) = -\lambda \frac {T_{cell} - T_c} {\delta}$

где $T_0, T_c, T_{cell}$ температура охлаждающей (нагревающей) среды, температура стенки и температура центра граничной ячейки, $\delta$ – расстояние от стенки до центра ячейки. Т.к. температура стенки и центра ячейки связаны, то вывести явно выраженную функцию не получится. Поэтому необходимо использовать следующую конструкцию:

$T_c = f T_0 + (1-f)(T_{cell} + {\nabla_\perp T} {\delta} )$

где f – функция веса, при f=1 получаем чистые ГУ 1-го рода (Дирихле), при f=0 получаем условия второго рода (Неймана). Получим чему равна функция веса в нашем случае:

$T_c = T_0 + \frac {\lambda}{\alpha \delta} ( T_{cell} - T_c)$
$T_c (1 + \frac {\lambda} {\alpha \delta} ) = T_0 + T_{cell} \frac {\lambda} {\alpha \delta}$
$T_c = \frac {1} {1 + \frac {\lambda} {\alpha \delta}} T_0 + (1 - \frac {1} {1+ \frac {\lambda}{\alpha \delta}}) T_{cell}$
Отсюда получаем $f= \frac {1} {1+\frac {\lambda}{\alpha \delta}}$ , а $\nabla_\perp T = 0$ , т.е нулевой градиент. Не буду присваивать чужую идею, подсмотрено здесь

Итак, отличия от примера №1 только в 0/T, куда встраиваем код:

right_wall
{
    // тип граничных условий    
    type                codedMixed;
    // значения при 0 (обычно нужно для paraFoam)
    // ГУ Дирихле
    refValue	        uniform 273.15;
    // ГУ Неймана
    refGradient	        uniform 0;
    // весовая функция f
    valueFraction	uniform 1;
    // название функции
    redirectType	qFixed;
	code
	#{
                // постоянные (здесь к сожалению нельзя их взять из include/initialConditions
		scalar q = 200;
		scalar lambda = 0.2;
                // новые значения условий неймана и дирихле
		this->refValue() = 0;
		this->refGrad() = q / lambda;
                // весовая функция для фиксированного градиента
		this->valueFraction() = 0;
	#};
    }
left_wall
{
	type		codedMixed;
        refValue        uniform 273.15;
        refGradient     uniform 0;
        valueFraction   uniform 1;
        redirectType    heatTransferCoef;
	code
	#{
                // постоянные
		scalar alpha=10;
		scalar T_flow=253.15;
		scalar lambda=0.2;
                // ГУ Дирихле
		this->refValue() =  T_flow;
                // ГУ Неймана
		this->refGrad() = 0;
                // получаем векторное поле расстояний от стенки ячейки до ее центра
		vectorField patchCf
		(
			this->;patch().delta()
		);
                // аналогичное скалярное поле (длины векторов)
		scalarField magPatchCf
		(
			mag(patchCf)
		);
                // вычисляем весовую функцию
		this->valueFraction() = 1.0/(1.0+lambda/(magPatchCf*alpha));
	#};

right_wall

{

// тип граничных условий

type codedMixed;

// значения при 0 (обычно нужно для paraFoam)

// ГУ Дирихле

refValue uniform 273.15;

// ГУ Неймана

refGradient uniform 0;

// весовая функция f

valueFraction uniform 1;

// название функции

redirectType qFixed;

code

// постоянные (здесь к сожалению нельзя их взять из include/initialConditions

scalar q = 200;

scalar lambda = 0.2;

// новые значения условий неймана и дирихле

this->refValue() = 0;

this->refGrad() = q / lambda;

// весовая функция для фиксированного градиента

this->valueFraction() = 0;

#};

}

left_wall

{

type codedMixed;

refValue uniform 273.15;

refGradient uniform 0;

valueFraction uniform 1;

redirectType heatTransferCoef;

code

// постоянные

scalar alpha=10;

scalar T_flow=253.15;

scalar lambda=0.2;

// ГУ Дирихле

this->refValue() = T_flow;

// ГУ Неймана

this->refGrad() = 0;

// получаем векторное поле расстояний от стенки ячейки до ее центра

vectorField patchCf

(

this->;patch().delta()

);

// аналогичное скалярное поле (длины векторов)

scalarField magPatchCf

(

mag(patchCf)

);

// вычисляем весовую функцию

this->valueFraction() = 1.0/(1.0+lambda/(magPatchCf*alpha));

#};

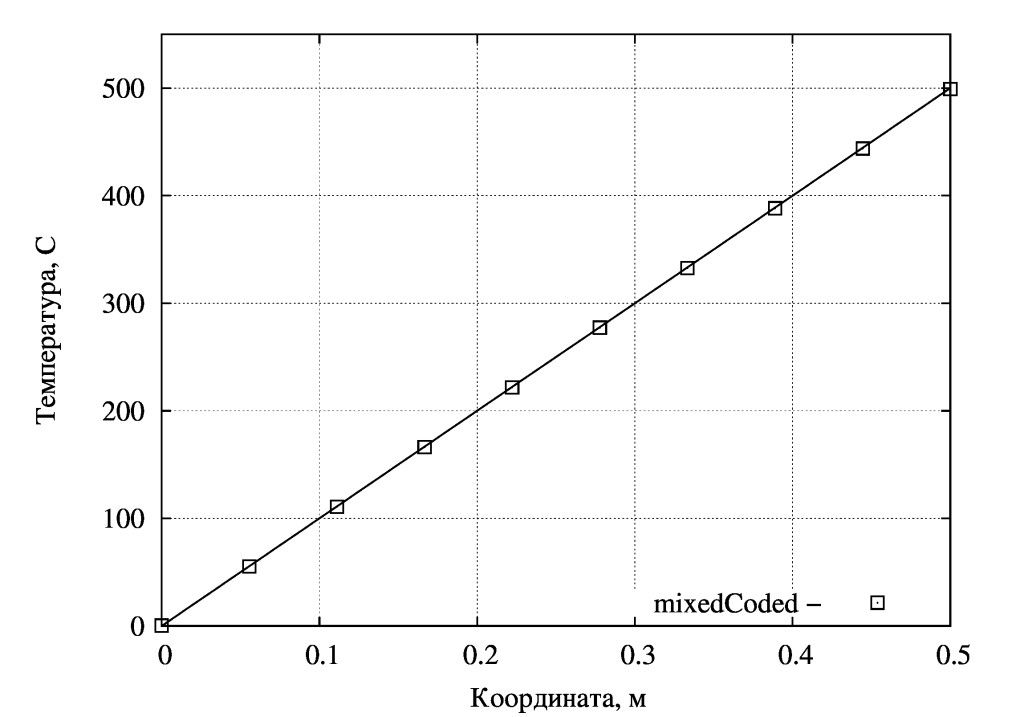
На рисунке ниже показано распределение температуры, все точно с расчетными значениями (0 С и 500 С).

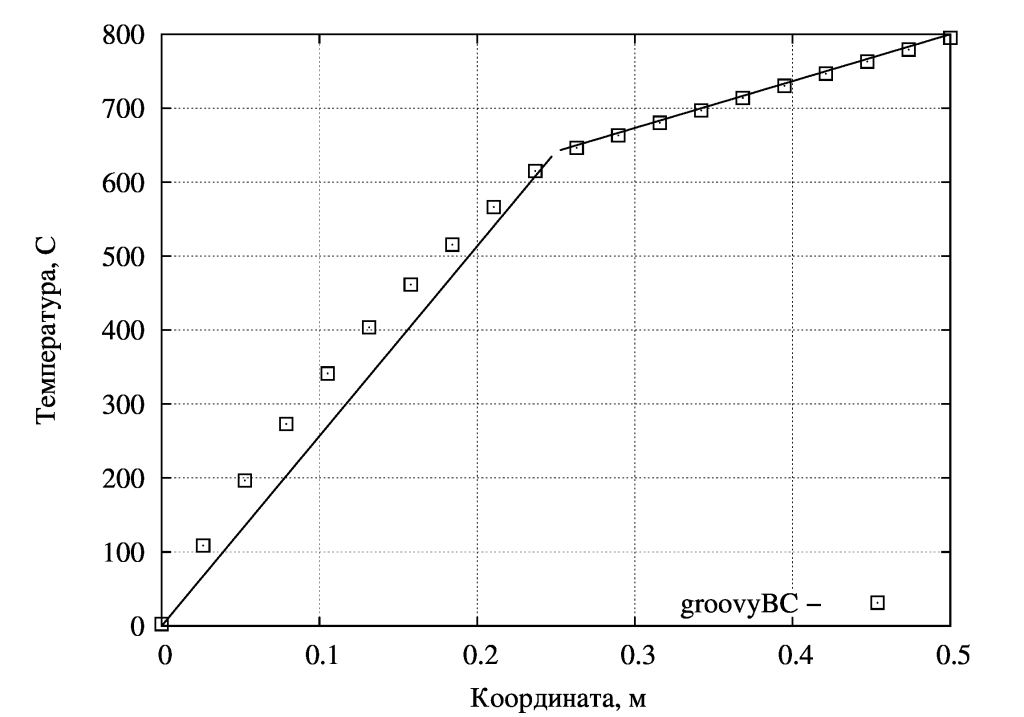
Далее рассмотрю, как задать ГУ 2-го и 3-го рода через groovyBC, что гораздо проще. Изменим пример №2. На одной стенке зададим тепловой поток q=899,47 Вт/м.кв, на другой стенке коэффициент теплоотдачи alpha=44,97 Вт/м.кв*С и температуру охлаждающей среды t=-20 C. Значения подобраны не абы как, а чтобы получить такое же распределение температур, т.е. температуры стенок 0 С и 800 С, температура между слоями – 641,7 С.
См. приложенный файл groovyBCMyLaplacianFoam.tar.gz
Итак, в чем изменения.
1. Добавим библиотеки в controlDict

// первая библиотека нужна для работы paraFoam, вторая непосредственно groovyBC
libs ("libOpenFOAM.so" "libgroovyBC.so" );

1 2	// первая библиотека нужна для работы paraFoam, вторая непосредственно groovyBC libs ("libOpenFOAM.so" "libgroovyBC.so" );

2. Отредактируем 0/T. В отличии от встраивания кода можно очень просто использовать переменные из include/initialConditions. Все аналогично расчетам выше, кроме учета влияния температуры на теплопроводность (значения b и T берутся прямо из расчета, что очень удобно).

left_wall
{
    value         uniform $internalT;
    type          groovyBC;
    variables     "lambda=$lambda_01*(1+b*(T-273.15));";
    valueExpression         "$T_flow";
    fractionExpression      "1.0/(1.0+lambda/(mag(delta())*$alpha))";
}

right_wall
{
    value                   uniform $internalT;
    type                    groovyBC;
    variables               "lambda=$lambda_02*(1+b*(T-273.15));";
    fractionExpression      "0";
    gradientExpression      "$q/lambda";
}

left_wall

{

value uniform $internalT;

type groovyBC;

variables "lambda=$lambda_01*(1+b*(T-273.15));";

valueExpression "$T_flow";

fractionExpression "1.0/(1.0+lambda/(mag(delta())*$alpha))";

}

right_wall

{

value uniform $internalT;

type groovyBC;

variables "lambda=$lambda_02*(1+b*(T-273.15));";

fractionExpression "0";

gradientExpression "$q/lambda";

}

На рисунке ниже опять сопоставление данных моделирования и аналитического расчета. Совпадает.

Блог Загоскина А.А.

Аэродинамика, теплообмен, cfd, OpenFOAM

Моделирование теплопроводности. Пример 3