Моделирование теплопроводности. Пример 1.

Моделирование нестационарной теплопроводности – наиболее простая задача теплообмена, решаемая с помощью численных методов. Особенно это просто сделать при простой геометрии, постоянной теплопроводности и граничных условиях первого рода. В разнообраных вычислительных платформах это делается при минимуме необходимых настроек и соответственно трудозатрат. В данной статье рассмотрен расчет в OpenFOAM охлаждения неограниченной пластины с температуропроводностью $10^{-6}$ м.кв/с, толщиной 0,5 м, находящейся в начальный момент времени при t=500 c, если мгновенно уменьшить температуру одной стенки до t=0 С. Также выполнено сопоставление с аналитическим расчетом.

Дифференциальное уравнение распространения теплоты теплопроводностью при отсутствии внутренних источников достаточно простое [1]:
$\frac {\partial T} {\partial \tau} = a \nabla ^2 T$
где $T$ – температура;
$\tau$ – время;
$a$ – температуропроводность;
$\nabla ^2$ – оператор Лапласа.
Код OpenFOAM в таком случае выглядит следующим образом [2]:

solve
(
     fvm::ddt(T) - fvm::laplacian(DT,T)
)

solve

(

fvm::ddt(T) - fvm::laplacian(DT,T)

)

Структура расположения папок и файлов в расчетной директории следующая (см. приложенный файл transientConduction.tar.gz):

0 (обязательная папка, в ней решатели ищут начальные условия необходимых переменных)
constant (обязательная папка, здесь располагаются: сетка, параметры модели турбулентности, теплофизические свойства и прочее неизменяющееся во времени)
system (обязательная папка, тут находятся конфигурационные файлы параметров дискретизации дифференциальных уравнений, параметры решателя и всех дополнительных утилит)
logs (папка не обязательна, как видно из названия в нее я обычно свожу все логи)
scripts (здесь я обычно размещаю все bash-скрипты для генерации сетки, пре- и пост- обработки, управления ходом расчета. Папка необязательна)

Для упрощения контроля правильности ввода начальных параметров, особенно если их много и серия опытов большая, я все исходные значения обычно свожу в один файл 0/include/initialConditions. В разбираемом примере необходимо задать только начальное распределение температуры 0/T:

//делаем ссылку на файл начальных значений
#include "include/initialConditions";
//размерность начального параметра [килограмм метр секунда кельвин килограмм-моль канделла]
dimensions [0 0 0 1 0 0 0];
//начальная внутренняя температура пластины, переменная $internalT задана в initialConditions
internalField uniform $internalT;
//граничные условия
boundaryField
{
    //пластина неограниченная, поэтому для задания 1D расчета на 4 гранях
    //исключаем теплообмен, задавая нулевой градиент температуры
    defaultFaces
    {
        type zeroGradient;
    }
    //далее фиксированные значения температур на стенках
    left_wall
    {
        type fixedValue;
        value uniform $wall_T_c;
    }
    right_wall
    {
        type fixedValue;
        value uniform $wall_T_0;
    }
}

//делаем ссылку на файл начальных значений

#include "include/initialConditions";

//размерность начального параметра [килограмм метр секунда кельвин килограмм-моль канделла]

dimensions [0 0 0 1 0 0 0];

//начальная внутренняя температура пластины, переменная $internalT задана в initialConditions

internalField uniform $internalT;

//граничные условия

boundaryField

{

//пластина неограниченная, поэтому для задания 1D расчета на 4 гранях

//исключаем теплообмен, задавая нулевой градиент температуры

defaultFaces

{

type zeroGradient;

}

//далее фиксированные значения температур на стенках

left_wall

{

type fixedValue;

value uniform $wall_T_c;

}

right_wall

{

type fixedValue;

value uniform $wall_T_0;

}

Аналогично поступаем и с constant/transportProperties

//вставляем файл с всеми начальными параметрами
#include "../0/include/initialConditions";
//задаем величину температуропроводности через переменную DT
//размерность соответственно м.кв/с
DT DT [ 0 2 -1 0 0 0 0 ] $DT;

//вставляем файл с всеми начальными параметрами

#include "../0/include/initialConditions";

//задаем величину температуропроводности через переменную DT

//размерность соответственно м.кв/с

DT DT [ 0 2 -1 0 0 0 0 ] $DT;

В папке constant/polyMesh находятся файлы расчетной сетки, которые генерируются утилитой blockMesh, которая обрабатывает constant/polyMesh/blockMeshDict. Если предполагается какое-либо изменение геометрических размеров сетки, то лучше сгенерировать blockMeshDict с помощью bash-скрипта. В данном случае он лежит в scripts/meshgen.sh. Правила создания сетки с помощью blockMesh достаточно понятно описаны здесь, в интернете есть полностью переведенный user guide.
Далее рассмотрим конфигурационные файлы в папке system. В файле system/controlDict задаются временные интервалы, вид результатов расчета, здесь же задаются параметры так называемого runTime-postprocessing.

//очевидно, что тут пишется, какое приложение будет запускаться
application laplacianFoam;
//с какого времени делать расчет. В нашем случае - с последнего имеющегося
startFrom latestTime;
//указываем где остановится
stopAt endTime;
endTime 50000;
//шаг по времени 200 секунд
deltaT 200;
//указываем, что результаты расчета записывать каждые 1000 секунд
writeControl runTime;
writeInterval 1000;
// результаты расчета не удалять
purgeWrite 0;
// формат сохраняемых файлов, нет необходимости менять
writeFormat ascii;
writePrecision 6;
writeCompression compressed;
timeFormat general;
timePrecision 6;
//возможность модификации данного файла "налету"
runTimeModifiable true;

//очевидно, что тут пишется, какое приложение будет запускаться

application laplacianFoam;

//с какого времени делать расчет. В нашем случае - с последнего имеющегося

startFrom latestTime;

//указываем где остановится

stopAt endTime;

endTime 50000;

//шаг по времени 200 секунд

deltaT 200;

//указываем, что результаты расчета записывать каждые 1000 секунд

writeControl runTime;

writeInterval 1000;

// результаты расчета не удалять

purgeWrite 0;

// формат сохраняемых файлов, нет необходимости менять

writeFormat ascii;

writePrecision 6;

writeCompression compressed;

timeFormat general;

timePrecision 6;

//возможность модификации данного файла "налету"

runTimeModifiable true;

Конфигурационный файл fvSchemes отвечает за дискретизацию дифференциальных уравнений. Теплопроводность – наверно самый простой случай, чистая диффузия, конвективных членов нет, самый сходимый вариант. Поэтому все довольно коротко:

//дискретизация нестационарных членов: неявное, первый порядок точности
ddtSchemes
{
    default Euler;
}
// центральноразностная схема (самая точная) для градиента и лапласиана
gradSchemes
{
    default Gauss linear;
}
laplacianSchemes
{
    default none;
    laplacian(DT,T) Gauss linear corrected;
}

//дискретизация нестационарных членов: неявное, первый порядок точности

ddtSchemes

{

default Euler;

}

// центральноразностная схема (самая точная) для градиента и лапласиана

gradSchemes

{

default Gauss linear;

}

laplacianSchemes

{

default none;

laplacian(DT,T) Gauss linear corrected;

}

Файл fvSolution отвечает за решение матриц уравнений и настройки самого решателя.

solvers
{
//каким образом решаем матрицу уравнений
    T
    {
        //решатель и предобуславливатель
        solver PCG;
        preconditioner DIC;
        //до какой точности будут решать матрицы
        tolerance 1e-08;
        //относительная точность между шагами
        relTol 0;
    }
}
{
    nNonOrthogonalCorrectors 2;
}

solvers

{

//каким образом решаем матрицу уравнений

{

//решатель и предобуславливатель

solver PCG;

preconditioner DIC;

//до какой точности будут решать матрицы

tolerance 1e-08;

//относительная точность между шагами

relTol 0;

}

{

nNonOrthogonalCorrectors 2;

}

Пишем простой скрипт для последовательного запуска

#!/bin/bash
// создаем необходимые папки
mkdir logs graphics;
//генерируем blockMeshDict
bash scripts/meshgen.sh &gt; constant/polyMesh/blockMeshDict;
//создаем расчетную сетку
blockMesh; logs/log.blockMesh;
//проверим сетку
checkMesh; logs/log.checkMesh;
//запускаем солвер
laplacianFoam; logs/log.laplacianFoam;
//удаляем ненужные результаты расчета
rm -r 2000 3000 4000 6000 7000 8000 9000 10000 11000 12000 13000 14000 16000 17000 18000 19000 20000 21000 22000 23000 24000 25000 26000 27000 28000 29000 30000 31000 32000 33000 34000 35000 36000 37000 38000 39000 40000 41000 42000 43000 44000 45000 46000 47000 48000 49000;
//получаем необходимые данные из результатов
sample; logs/log.sample;
//строим график
gnuplot scripts/plot.gnu;
//конвертируем полученный *.eps файл в *.png
for i in *.eps
    do
    name=`echo $i | sed 's/.eps//g'`;
    convert -density 460 -background white -flatten +matte $i graphics/$name.png;
    rm -r $i;
done;

#!/bin/bash

// создаем необходимые папки

mkdir logs graphics;

//генерируем blockMeshDict

bash scripts/meshgen.sh > constant/polyMesh/blockMeshDict;

//создаем расчетную сетку

blockMesh; logs/log.blockMesh;

//проверим сетку

checkMesh; logs/log.checkMesh;

//запускаем солвер

laplacianFoam; logs/log.laplacianFoam;

//удаляем ненужные результаты расчета

rm -r 2000 3000 4000 6000 7000 8000 9000 10000 11000 12000 13000 14000 16000 17000 18000 19000 20000 21000 22000 23000 24000 25000 26000 27000 28000 29000 30000 31000 32000 33000 34000 35000 36000 37000 38000 39000 40000 41000 42000 43000 44000 45000 46000 47000 48000 49000;

//получаем необходимые данные из результатов

sample; logs/log.sample;

//строим график

gnuplot scripts/plot.gnu;

//конвертируем полученный *.eps файл в *.png

for i in *.eps

name=`echo $i | sed 's/.eps//g'`;

convert -density 460 -background white -flatten +matte $i graphics/$name.png;

rm -r $i;

done;

Аналитический расчет данного случая можно посмотреть в работе [1] и выглядит следующим образом:
$\theta = \frac {x} {R} + \sum_{n=1} ^ \infty {(-1)^{n+1} \frac {2} {\mu _n} \sin (\mu _n) \frac {R-x} {R} \exp (- \mu _n ^2 Fo)}$
где $\theta = \frac { T(x,\tau) - T_c} {T_0 - T_c}$ – безразмерный температурный напор;
$\mu _n=n \pi$ – характеристические числа;
$R$ – толщина пластины;
$Fo=\frac {a \tau} {R^2}$ – число Фурье.
Достаточно использовать n=1…9.
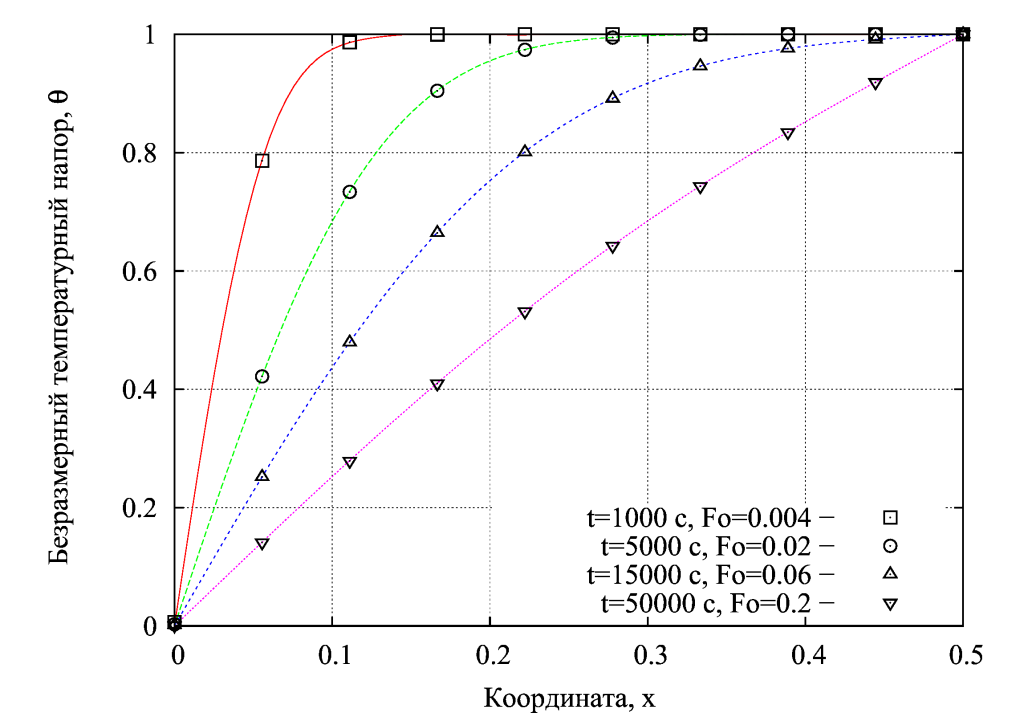
На графике выполнено сопоставление профилей температурного напора в разные моменты времени. Линиями обозначены аналитические решения, значками – численное.

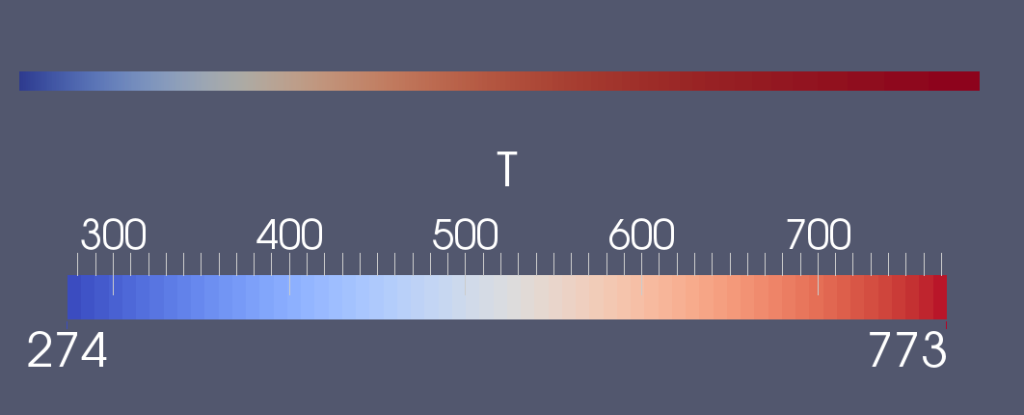
Рисунок ниже показывает распределение абсолютной температуры в один из моментов времени (t=15000 c).
plot_X

Источники:
1. Лыков А.В. Теория теплопроводности. – Изд-во “Высшая школа”, 1967 г. – 600 с.
2. applications/solvers/basic/laplacianFoam/laplacianFoam.C

Блог Загоскина А.А.

Аэродинамика, теплообмен, cfd, OpenFOAM

Моделирование теплопроводности. Пример 1.