При расчете теплообмена излучением часто возникает проблема с нахождением угловых коэффициентов, которые представляют собой геометрическую характеристику взаимного положения двух поверхностей в пространстве. Если случай какой-нибудь из простых, например, соосные квадрат и круг и пр., аналитически найти угловые коэффициенты никаких трудностей не вызывает. Однако, когда мы имеем сложные криволинейные поверхности в объеме, задача становится нетривиальной и требует численных методов. В openFoam есть для этого специальная утилита viewFactorsGen, которую мы в данной статье протестируем на простейшем случае: куб внутри цилиндра с длиной L=D.

См. далее
Архив рубрики: OpenFOAM
Моделирование аэродинамики циклонных устройств. Часть 2.
Продолжу рассматривать численное моделирование аэродинамики циклонных устройств. Начало здесь. Как я отмечал ранее, использование “классических” моделей турбулентности kOmegaSST и SA в их первоначальном виде приводит к завышению турбулентной вязкости и значительному смещению максимума тангенциальной скорости к боковой поверхности камеры. В данной статье введем в эти модели поправки на кривизну линий тока и сравним полученные профили безразмерной тангенциальной скорости с экспериментальными.
См. далее
Моделирование аэродинамики циклонного устройства. Часть 1.
Именно с этой темы я и начинал знакомиться с openFoam-ом и численным моделированием. Задача оказалась абсолютно нетривиальной из-за сильно закрученного течения, образующегося в циклонном устройстве. На каждом форуме, посвященном ВГД, обязательно можно найти тему про данную задачу, например на cfd-online.com: 1, 2. Были и на форуме os-cfd.ru хорошие темы по моделированию циклонов, но форум куда-то пропал.
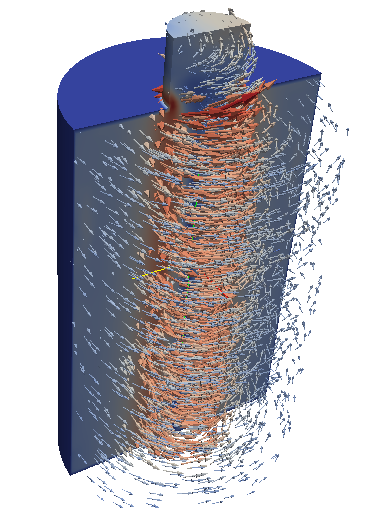
В данной статье я рассмотрю решение рассматриваемой задачи при использовании модели турбулентности Лаундера-Гибсона (LaunderGibsonRSTM);
См. далее
Обтекание цилиндра. Конвективный теплообмен.
Начало здесь.
Продолжу рассматривать численное моделирование конвективного теплообмена. В данной статье решим задачу поперечного обтекания цилиндра потоком воздуха. Рассмотрим следующие вопросы:
1) Получим численно средний коэффициент теплоотдачи от трубки диаметром d=15 мм при числе Рейнольдса Re=1000…15000, температура трубки 100 С, температура потока 0 С;
2) Выполним сопоставление полученных значений с имеющимися в литературе обобщающими зависимостями [1];
3) Сопоставим средние тепловые потоки от трубки, найденные через градиент температуры в ламинарном подслое трубки и через перепад температуры на входе и выходе канала;
4) Сопоставим распределение среднего коэффициента теплоотдачи по периметру трубки с экспериментальными значениями [2].
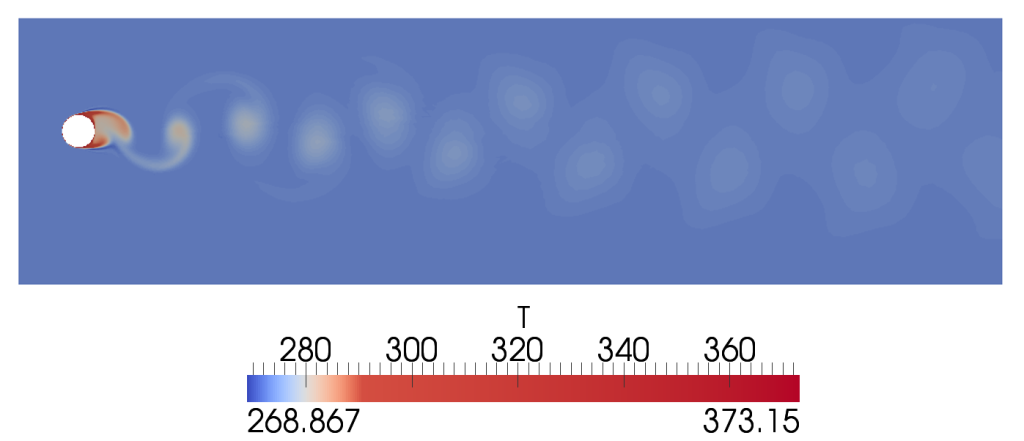
См. далее
Турбулентное течение в трубе. Конвективный теплообмен.
С данной статьи я начну рассматривать численное моделирование конвективного теплообмена. Самый простой случай – турбулентное течение в трубе. Определим средний по поверхности коэффициент теплоотдачи, распределение коэффициента теплоотдачи по длине трубы и сопоставим с обобщающими расчетными зависимостями [1,2]. Диаметр трубы d=15 мм, длина L=150 мм выбрана такой, чтобы взять точное значение поправки на начальный участок. Температура стенки задавалась равной 100 С, начальная температура потока – 0 С. Скорость на входе принимала значения U=10.187; 20.373; 50.9333.
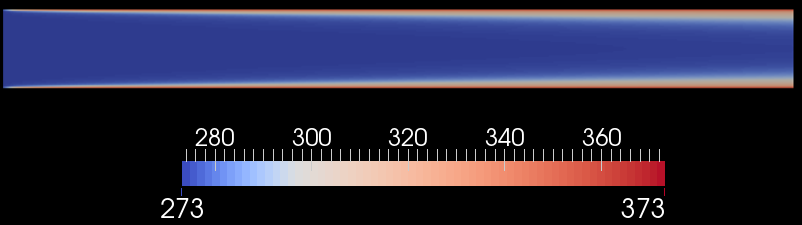
См. далее
Обтекание цилиндра. Re=400…1200
Продолжение, начало см:
Обтекание цилиндра. Re=1…30
Обтекание цилиндра. Re=100…200
Обтекание цилиндра в диапазоне Re>400 идет в турбулентном нестационарном режиме, все также образуется вихревая дорожка Кармана:

Основы моделирования турбулентности, модели турбулентности и области применимости наиболее удачно описаны в следующих книгах [1,2]. Вообще моделей турбулентности очень-очень много, но универсальной до сих пор нет, и видимо не появится. Наиболее распространенные на сегодня – модель Спаларта-Алмараса, и модель k-omega-SST Ментера, они обкатаны на большом спектре задач и их можно использовать “по умолчанию” в большинстве случаев. Модель k-epsilon уже очень старая, есть множество ее модификаций, в этой статье я буду использовать наиболее удачную модификацию Лаундера-Шармы, просто в качестве возможной альтернативы.
Есть мнение, что модель Спаларта-Алмараса нужно использовать в случае внешних задач, а модель k-omega-SST для внутренних, видимо так сложилось исторически, но я до сих пор не нашел этому подтверждение. При внешних задачах, несмотря на развитие пристенных функций, я всегда стараюсь использовать низкорейнольдсовые модели турбулентности и ближайшую ячейку располагать при y+<1, это всегда повышает точность, и потом не приходится мучаться поиском причин расхождения опыта и эксперимента.
См. далее
Обтекание цилиндра. Re=100…200
См. обтекание цилиндра при Re=1…30
Теперь рассмотрим обтекание цилиндра при Re=100…200, как известно в данном случае образуется вихревая дорожка Кармана при ламинарном течении. Т.е. для получения нужной картины вихрей необходимо использовать нестационарный метод. В данной статье выполним следующее:
1) Получим картину вихревой дорожки Кармана:

2) Определим изменение числа Струхаля от числа Рейнольдса (St=f(Re)) и сопоставим с эмпирической зависимостью;
3) Продолжим получение зависимости Cd=f(Re).
Особенность получения вихревой дорожки Кармана с помощью icoFoam – введение некоторой несимметричности. Иначе получится стационарный след, аналогичный вихрям Твина.
Обтекание цилиндра. Re=1…30
Как известно, режим обтекания цилиндра зависит от числа Рейнольдса:
1) При Re=5…30 наблюдается образование вихрей Твина. Режим ламинарный, стационарный.
2) При Re=100…200 наблюдается вихревая дорожка Кармана. Режим ламинарный, нестационарный.
3) При Re>400 наблюдается вихревая дорожка Кармана. Режим турбулентный, нестационарный.
В данной статье рассмотрим п.1, ламинарное стационарное обтекание цилиндра диаметром d15 и числах Рейнольдса Re=1;5;15;30. Определим коэффициент полного сопротивления и сравним с имеющимися опытными данными.

См. далее
Стационарное ламинарное течение в трубе
В данной статье рассмотрю каким образом считается простейшее течение. В качестве примера возьмем течение на начальном участке трубы. Отсутствие необходимости определять турбулентные характеристики значительно упрощает задачу, т.к. решается обычное уравнение Навье-Стокса, без турбулентной вязкости или напряжений Рейнольдса:
где V – скорость потока, p – давление, F – массовые силы, t – время, – плотность,
– молекулярная вязкость.
В статье сделаем следующее:
1) Сопоставим численное и аналитическое решение увеличения скорости на оси трубы;
2) Сопоставим параболический профиль с профилем скорости после смыкания пограничных слоев;
3) Сравним скорость расчета при использовании различных методов решения матриц.
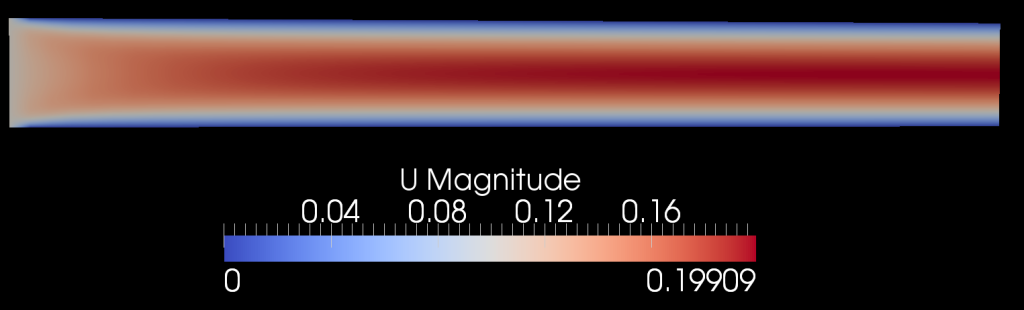
См. далее
Моделирование теплопроводности. Пример 3
Как я говорил ранее, граничные условия первого рода (фиксированная температура стенки) встречается на практике реже, чем условия третьего рода (через коэффициент теплоотдачи). В данной статье я покажу как использовать ГУ второго и третьего рода в openFoam при моделировании теплопроводности при использовании встроенных средств и сторонней библиотеки groovyBC.
Когда я впервые установил openFoam (была версия 1.8), встроенных средств для задания коэффициента теплоотдачи на поверхности не было, это можно было сделать только с помощью сторонней библиотеки groovyBC. Сейчас появилась возможность включать целые куски кода практически в любые места (ГУ, controlDict, blockMeshDict и пр.), что интересно с точки зрения освоения платформы, но на практике зачастую это удобней сделать все также через функции swak4foam. Встроенных граничных условий для задания коэффициента теплоотдачи все также нет.
Сначала я покажу на основе примера №1 возможности встраивания кода в 0/T. См. приложенный файл codedMixedLaplacianFoam.tar.gz. Найдем установившееся распределение температуры в бесконечной пластине (толщина 0,5 м, температуропроводность 1,33e-6 м.кв/с, теплопроводность 0,2 Вт/м*С) при задании граничных условий 3-го рода на одной стенке (температура охлаждающей среды -20 С, коэффициент теплоотдачи 10 Вт/(м.кв*С), и ГУ 2-го рода на другой (тепловой поток 200 Вт). Все значения специально подобраны, чтобы на одной стенке была температура 0 С, на второй 500 С.
См. далее