Начало здесь.
Продолжу рассматривать численное моделирование конвективного теплообмена. В данной статье решим задачу поперечного обтекания цилиндра потоком воздуха. Рассмотрим следующие вопросы:
1) Получим численно средний коэффициент теплоотдачи от трубки диаметром d=15 мм при числе Рейнольдса Re=1000…15000, температура трубки 100 С, температура потока 0 С;
2) Выполним сопоставление полученных значений с имеющимися в литературе обобщающими зависимостями [1];
3) Сопоставим средние тепловые потоки от трубки, найденные через градиент температуры в ламинарном подслое трубки и через перепад температуры на входе и выходе канала;
4) Сопоставим распределение среднего коэффициента теплоотдачи по периметру трубки с экспериментальными значениями [2].


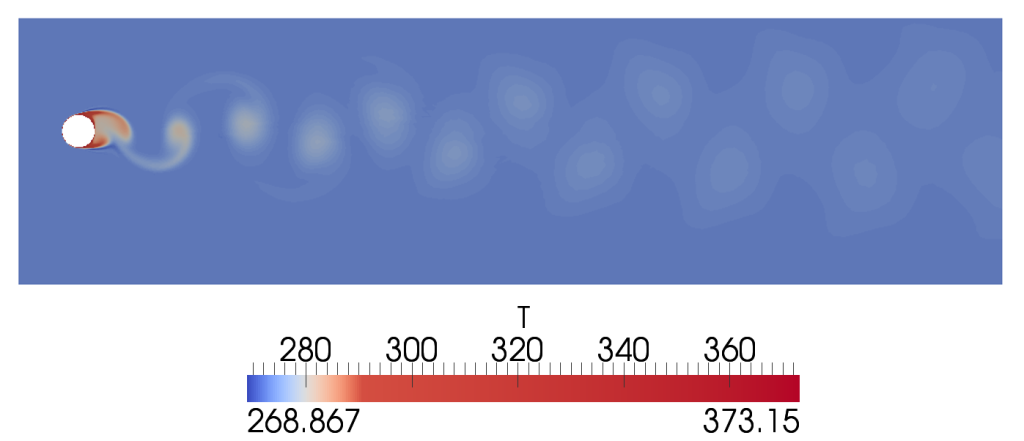
Режим обтекания нестационарный, используем солвер buoyantBoussinesqPimpleFoam. Т.к. коэффициент теплоотдачи изменяется синусоидально, необходимо использовать какую-либо run-time post-processing функцию определения суммарного теплового потока. Это можно сделать либо через groovyBC, либо встраивать код. В нашем случае сделаем это через groovyBC двумя различными способами:
1) через градиент температуры в ламинарном подслое вблизи поверхности цилиндра;
2) через перепад среднемассовой температуры на входе в канал и его выходе.
В первом случае встраиваемый в controlDict код имеет следующий вид (аналогичный утилите расчета суммарного теплового потока из предыдущего примера ):

В случае определения среднемассовой температуры потока “на лету” уже есть готовая функция в groovyBC и ничего городить не надо. Следует только указать поверхности и скалярное поле для осреднения:

В controlDict необходимо добавить библиотеки groovyBC и заинклудить файлы с runTime функциями:

Расчетная сетка взята из предыдущих примеров с обтеканием трубки, остальные настройки комментировать нет необходимости, как мне кажется. См. приложенные файлы: heatTurbulentKarmanVortexStreet.tar
Как видно из приведенного ниже графика, изменение суммарного теплового потока во времени происходит синусоидально, для расчета используем среднее между максимальным и минимальным значениями.

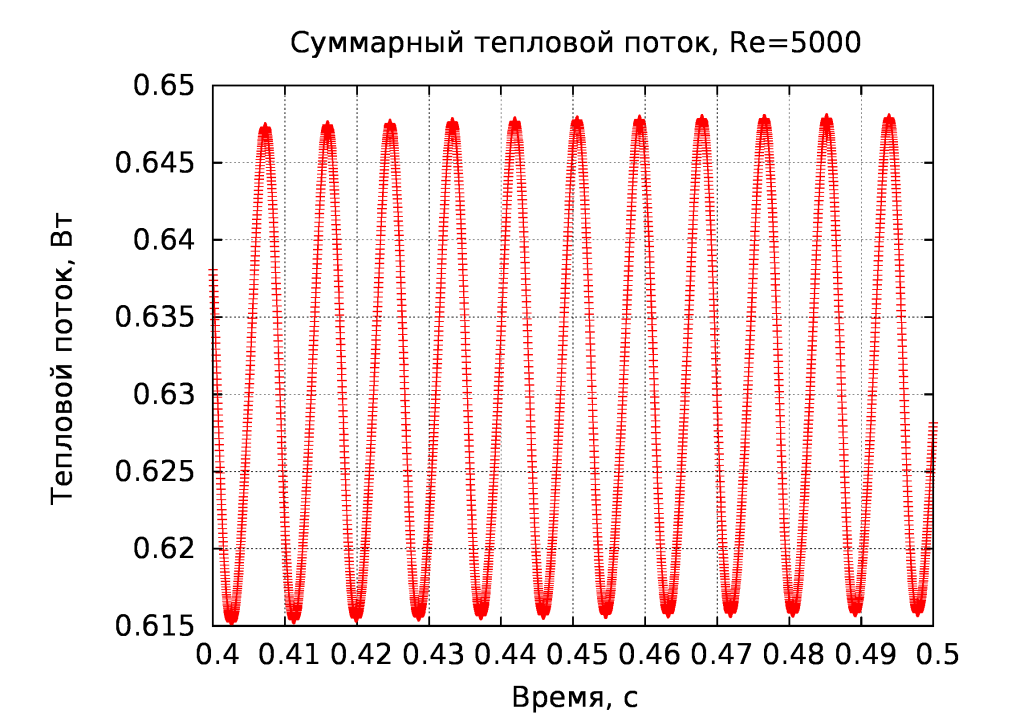
Аналогично поступаем и в случае среднемассовой температуры на выходе из канала:

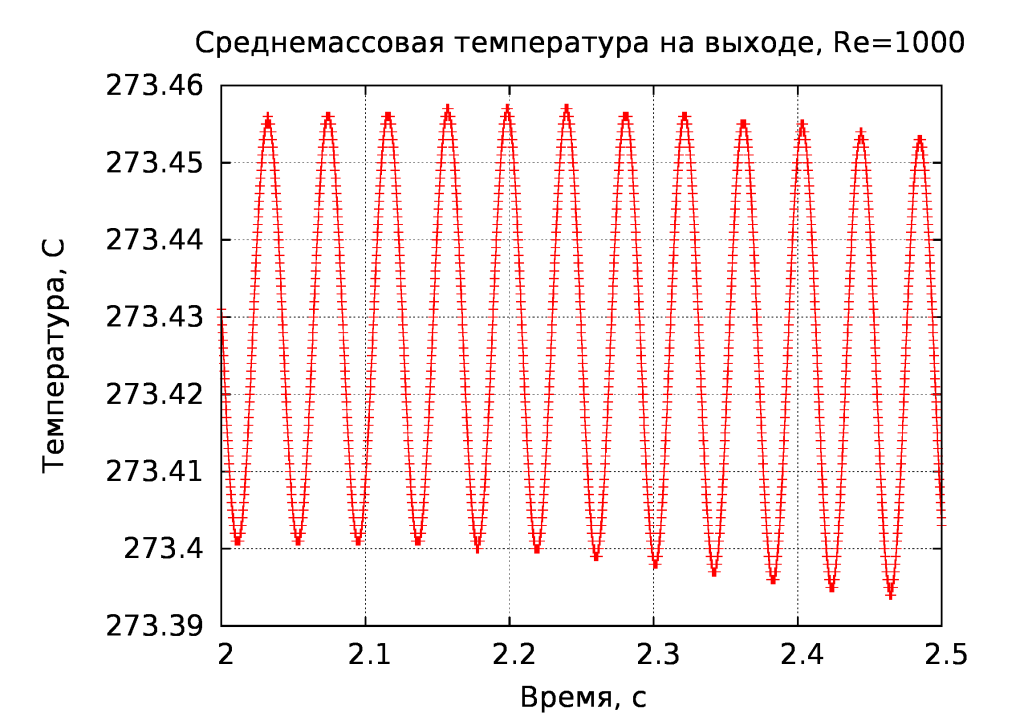
Отклонение значений суммарного теплового потока, рассчитанных двумя методами составляют:
при Re=1000 – 1.2%
при Re=5000 – 3.0%
при Re=10000 – 3.1%
при Re=15000 – 4.1%.

На рисунке ниже выполнено сопоставление числа Нуссельта, полученного численно с обобщающей эмпирической зависимостью из [1]. Максимальное отклонение составляет – 8.9%.

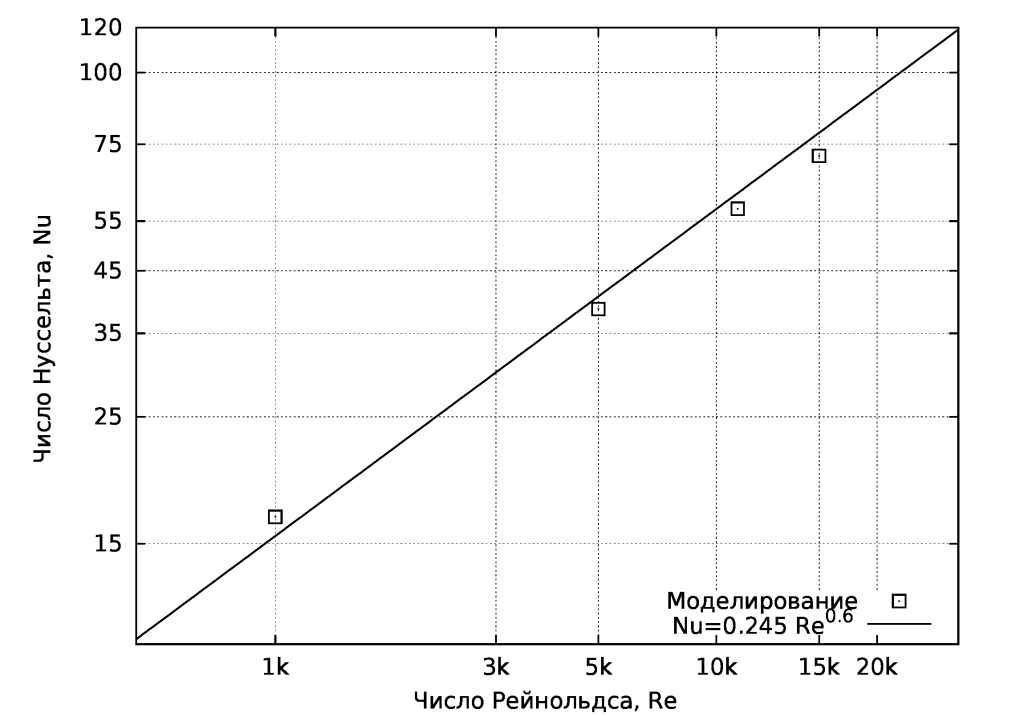
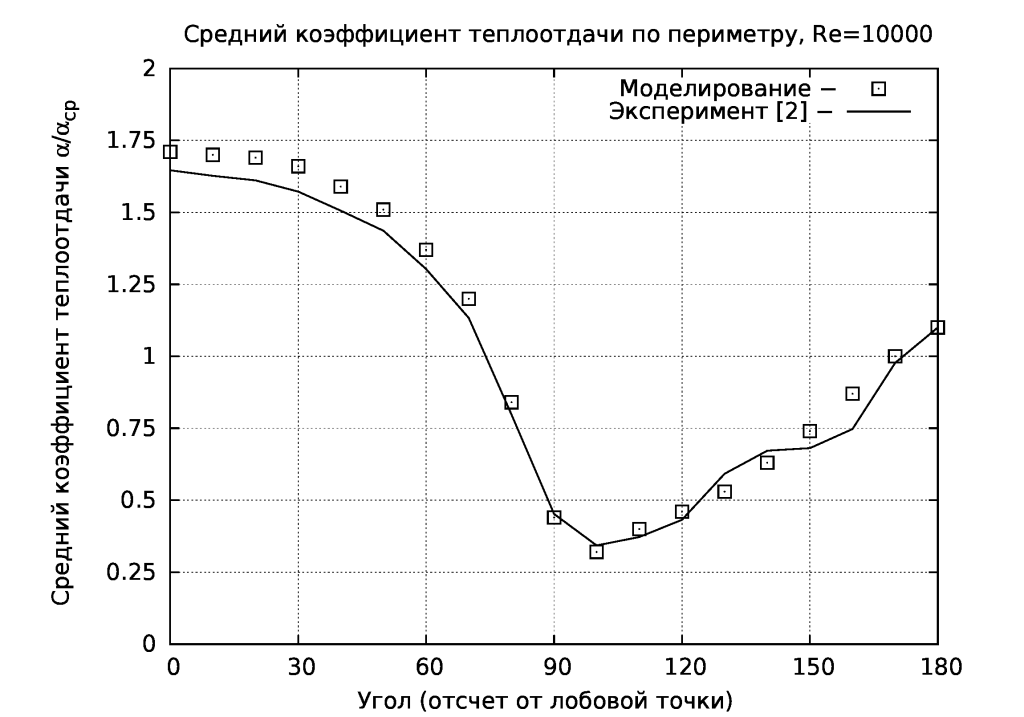
Сопоставление локальных средних коэффициентов теплоотдачи при Re=10000 выполнено с на рисунке ниже. Сопоставление удовлетворительное.

Литература:
1. Исаченко В.П. Телпопередача. 4-е изд., / В.П. Исаченко, В.А. Осипова, А.С. Сукомел – М.: Энергоатомиздат, 1981. – 416 с.
2. Кружилин Г.П. Новый метод определения поля коэффициента теплоотдачи на поверхности тела, омываемого потоком жидкости. / Г.П. Кружилин, В.А. Шваб – ЖТФ, 1935 – С.703-710