Обтекание цилиндра. Re=1…30 | Блог Загоскина А.А.

Как известно, режим обтекания цилиндра зависит от числа Рейнольдса:
1) При Re=5…30 наблюдается образование вихрей Твина. Режим ламинарный, стационарный.
2) При Re=100…200 наблюдается вихревая дорожка Кармана. Режим ламинарный, нестационарный.
3) При Re>400 наблюдается вихревая дорожка Кармана. Режим турбулентный, нестационарный.

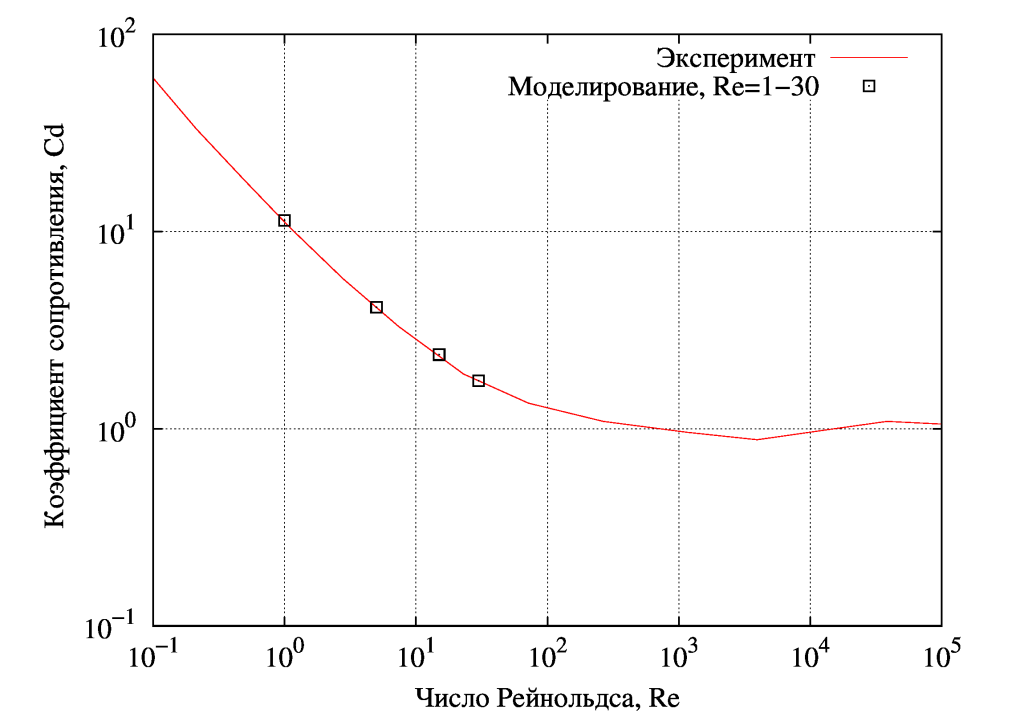
В данной статье рассмотрим п.1, ламинарное стационарное обтекание цилиндра диаметром d15 и числах Рейнольдса Re=1;5;15;30. Определим коэффициент полного сопротивления $C_D$ и сравним с имеющимися опытными данными.

Как известно $C_D$ определяется следующим образом:
$C_D = \frac {F_D} {\frac {1}{2} \rho_{inf} U_{inf}^2 A}$
где $F_D$ – сила действующая на цилиндр в направлении движения потока, состоящая действия силы трения и давления;
$\rho_{inf}$ , $U_{inf}$ – плотность и скорость невозмущенного потока;
$A$ – площадь поперечного сечения;

См. приложенный файл laminarTwinVortex.tar.gz
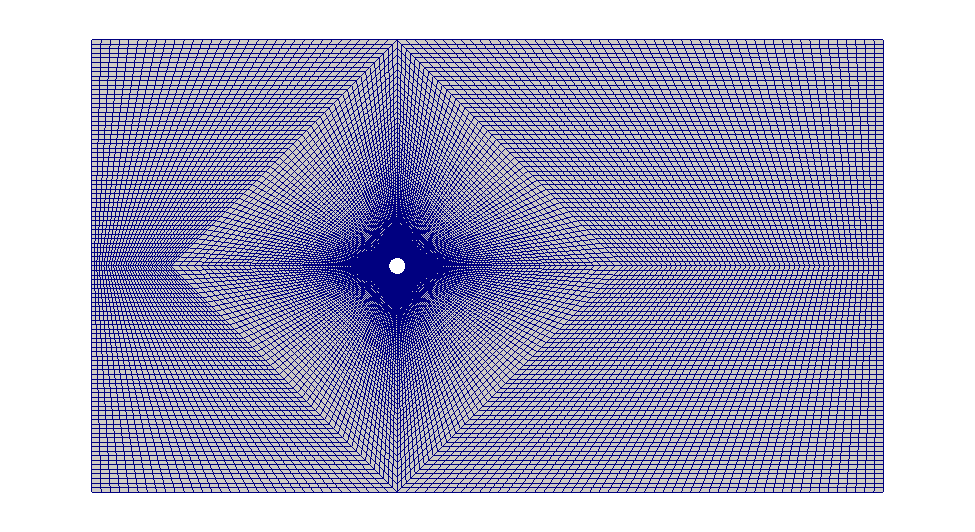
Расчетную сетку все также сгенерируем с помощью blockMesh. Вблизи цилиндра происходит значительное изменение скорости – поэтому дополнительно измельчаем. Пример расчетной сетки показан ниже:

Разницы в fvSchemes и fvSolution от предыдущего примера нет. Для вычисления коэффициента полного сопротивления добавим в controlDict следующую строку, которая отвечает за расчет Cd “на лету”:

functions
(
        #include "forceCoeffs"
);

functions

(

#include "forceCoeffs"

);

Сам system/forceCoeffs выглядит следующим образом:

forces
{
    type        forceCoeffs;
//подключаем необходимую библиотеку
    functionObjectLibs ( "libforces.so" );
// устанавливаем временной интенрвал для вычисления
    outputControl timeStep;
    outputInterval 5;
// для каких поверхностей вычислять
    patches     ( cylinder );
// имена для полей скорости и давления
    pName       p;
    UName       U;
// задаем перменную для плотности
    rhoName     rhoInf;
    log         true;
    rhoInf      1.204;
// направление подъемной силы
    liftDir     (0 0 1);
// направление потока
    dragDir     (1 0 0);
// скорость невозмущенного потока
    magUInf     0.03;
// "видимая" поверхность
    Aref        0.00003;
// в нашем случае не требуется
    CofR        (0 0 0);
    pitchAxis   (0 1 0);
    lRef        0.015;
}

forces

{

type forceCoeffs;

//подключаем необходимую библиотеку

functionObjectLibs ( "libforces.so" );

// устанавливаем временной интенрвал для вычисления

outputControl timeStep;

outputInterval 5;

// для каких поверхностей вычислять

patches ( cylinder );

// имена для полей скорости и давления

pName p;

UName U;

// задаем перменную для плотности

rhoName rhoInf;

log true;

rhoInf 1.204;

// направление подъемной силы

liftDir (0 0 1);

// направление потока

dragDir (1 0 0);

// скорость невозмущенного потока

magUInf 0.03;

// "видимая" поверхность

Aref 0.00003;

// в нашем случае не требуется

CofR (0 0 0);

pitchAxis (0 1 0);

lRef 0.015;

}

Как видно из поля скоростей, за цилиндром образуется та самая пара вихрей Твина:

Соответствие расчетных и экспериментальных значений Cd хорошое: