Обтекание цилиндра. Re=100…200 | Блог Загоскина А.А.

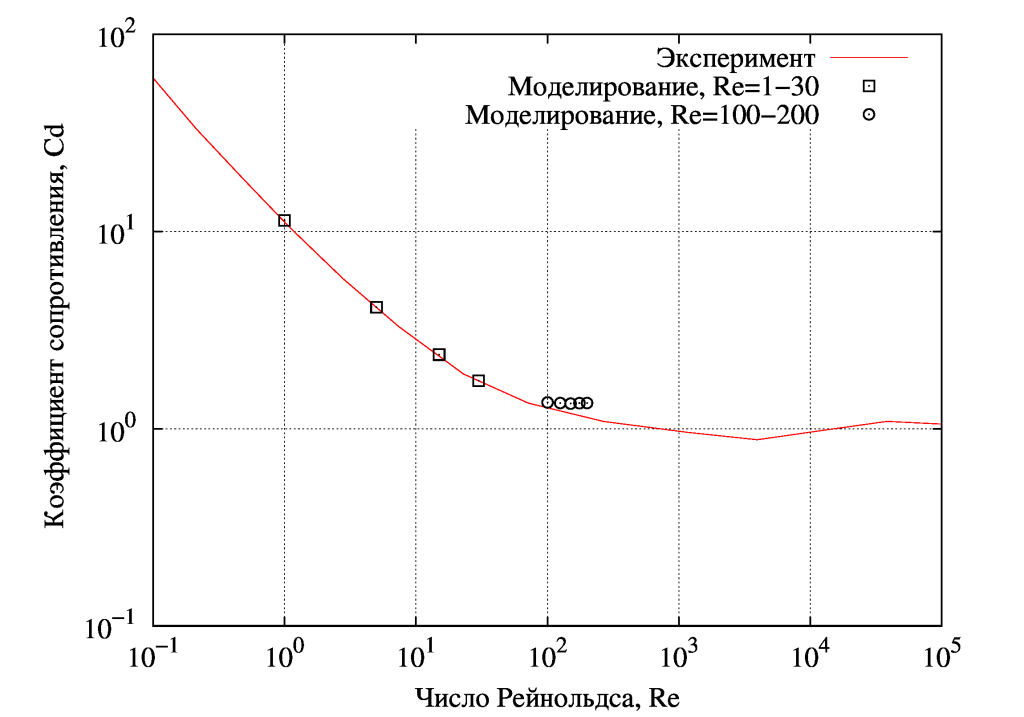
См. обтекание цилиндра при Re=1…30
Теперь рассмотрим обтекание цилиндра при Re=100…200, как известно в данном случае образуется вихревая дорожка Кармана при ламинарном течении. Т.е. для получения нужной картины вихрей необходимо использовать нестационарный метод. В данной статье выполним следующее:
1) Получим картину вихревой дорожки Кармана:

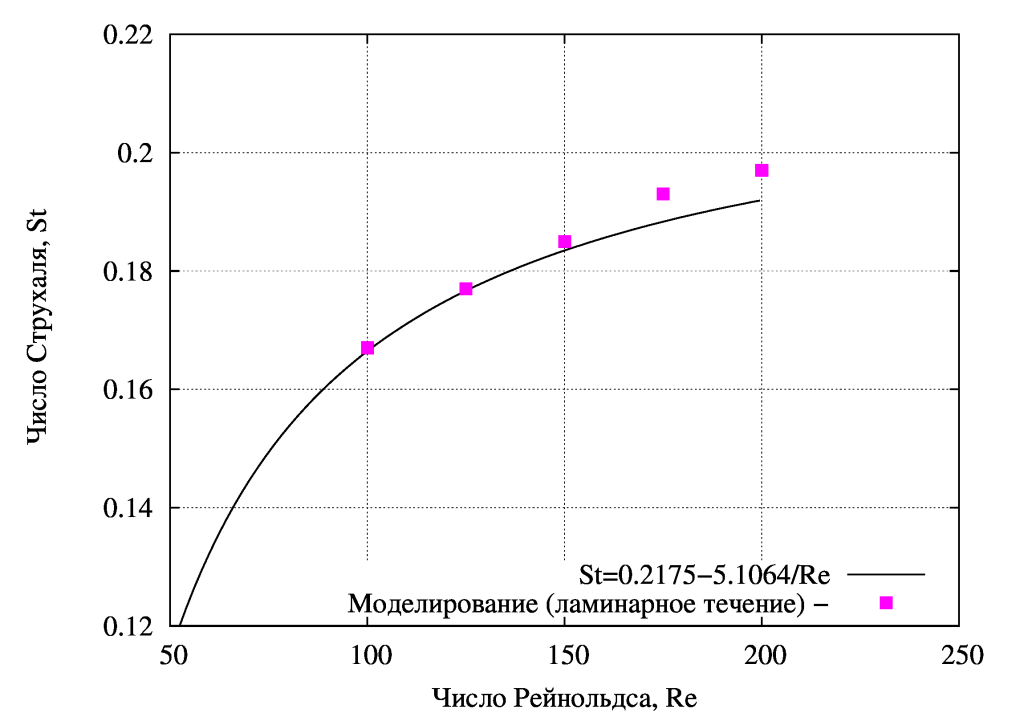
2) Определим изменение числа Струхаля от числа Рейнольдса (St=f(Re)) и сопоставим с эмпирической зависимостью;
3) Продолжим получение зависимости Cd=f(Re).
Особенность получения вихревой дорожки Кармана с помощью icoFoam – введение некоторой несимметричности. Иначе получится стационарный след, аналогичный вихрям Твина.

См. приложенный файл laminarKarmanVortexStreet.tar.gz
В данной статье для введения нестабильности используем кратковременное изменение вектора входной скорости, а именно:
В 0/U

    inlet
    {
        // изменение величины скорости по таблице
        type            uniformFixedValue;
        uniformValue    table
        (
                // начальный режим
                (0              ($U 0 0))
                ($time_1        ($U 0 0))
                // изменяем кратковременно вектор скорости
                ($time_2        ($U_attack_x $U_attack_y 0))
                ($time_3        ($U_attack_x $U_attack_y 0))
                // и снова на нормальный режим
                ($time_4        ($U 0 0))
                (4              ($U 0 0))
        );
    }

inlet

{

// изменение величины скорости по таблице

type uniformFixedValue;

uniformValue table

(

// начальный режим

(0 ($U 0 0))

($time_1 ($U 0 0))

// изменяем кратковременно вектор скорости

($time_2 ($U_attack_x $U_attack_y 0))

($time_3 ($U_attack_x $U_attack_y 0))

// и снова на нормальный режим

($time_4 ($U 0 0))

(4 ($U 0 0))

);

}

Переменные $U_attack_x $U_attack_y $time_* берутся из 0/include/initialConditions.
Изменяем схему дискретизации времени в system/fvSchemes:

ddtSchemes
{
    default         backward;
}

ddtSchemes

{

default backward;

}

В итоге получаем следующую анимацию, видно волну несимметричности, после которой образуются красивая дорожка вихрей:

Вихревая дорожка Кармана
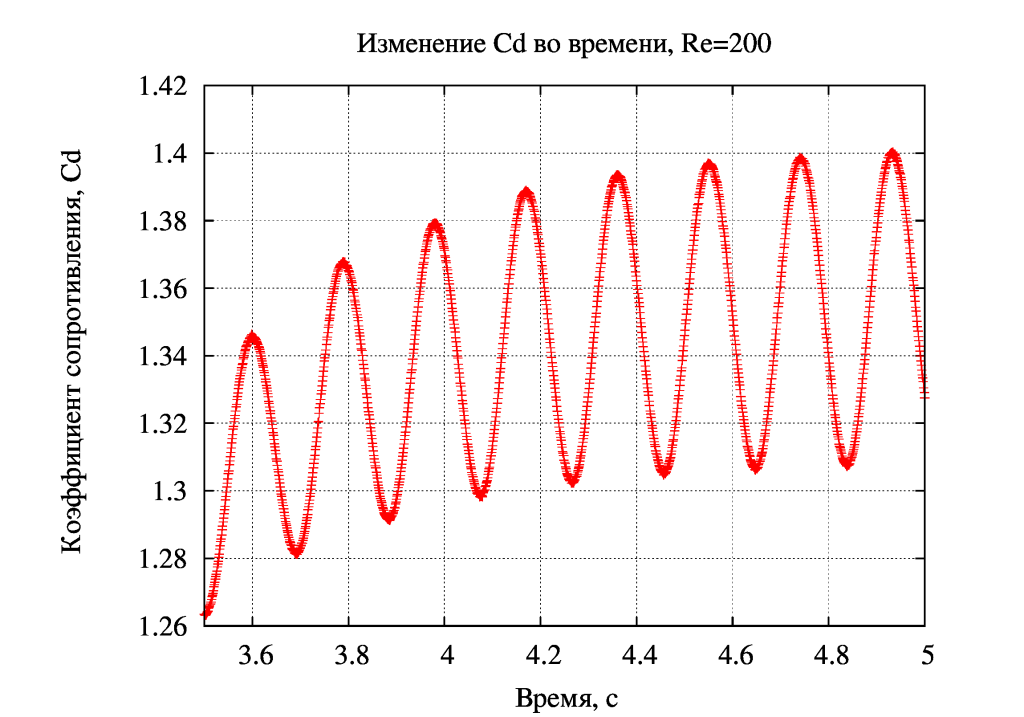
Число Струхаля определим по колебаниям коэффициента полного сопротивления Cd, который изменяется в 2 раза быстрее, чем происходит срыв вихрей, см. файл ниже, на котором изображено изменение Cd во времени при Re=200:

Сопоставление зависимости числа Струхаля и расчетных данных удовлетворительное. Разброс при Re=200, 2.4%.

Сопоставление по Cd=f(Re) хуже чем при Re=1..30: