С данной статьи я начну рассматривать численное моделирование конвективного теплообмена. Самый простой случай – турбулентное течение в трубе. Определим средний по поверхности коэффициент теплоотдачи, распределение коэффициента теплоотдачи по длине трубы и сопоставим с обобщающими расчетными зависимостями [1,2]. Диаметр трубы d=15 мм, длина L=150 мм выбрана такой, чтобы взять точное значение поправки на начальный участок. Температура стенки задавалась равной 100 С, начальная температура потока – 0 С. Скорость на входе принимала значения U=10.187; 20.373; 50.9333.


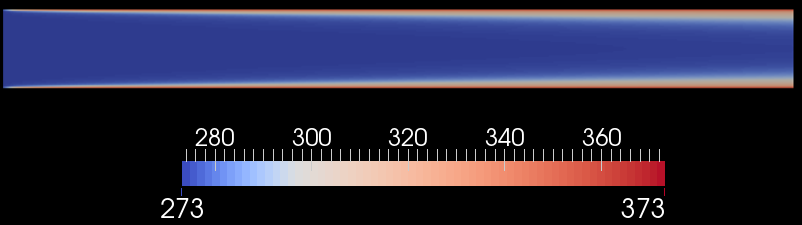
Будем использовать модель турбулентности kOmegaSST и солвер buoyantBoussinesqSimpleFoam. Как выполнить расчет начальных значений k и omega можно посмотреть здесь
Отличие от обычных simpleFoam и pimpleFoam заключается в решении дополнительного уравнения энергии:

где – эффективная температуропроводность (сумма физической и турбулентной температуропроводности);
Солвер buoyantBoussinesqSimpleFoam (*PimpleFoam) не учитывает сжимаемость газа используется в случае слабой изотермичности и малых числах Маха и обычно применяется для свободной конвекции. В нашем случае температурный напор и уровень скоростей небольшие, поэтому сжимаемостью можно принебречь, в противном случае надо использовать rhoSimpleFoam и rhoPimpleFoam. Однако учет сжимаемости серьезно усложняет задачу и на сложных геометриях может приводить к неустойчивости.
Турбулетная температуропроводность вычисляется через турбулентную вязкость и турбулетное число Прадтля, которое принимается постоянным и задается в constant/transportProperties (Prt=0.9).
Расчет теплового потока от стенки трубы можно выполнить тремя различными способами:
1) Обеспечить для первой ячейки y+<1 и в таком случае, тепловой поток можно найти как: [latex] q=\lambda \cdot grad(T) = C_p \cdot \rho \cdot a \cdot grad(T) [/latex] где [latex]\lambda , C_p , \rho, a[/latex] - теплопроводность, теплоемкость, плотность и температуропроводность газа; 2) Определить перепад температуры до и после трубы, отсюда можно найти средний тепловой поток; 3) Решить "смешанную" задачу аэродинамики и теплопроводности. В таком случае труба должна иметь некоторую твердую стенку, на внешней поверхности которой задавалась температура, а на внутренней она бы рассчитывалась. Зная перепад температуры и теплопроводность материала трубы можно также определить тепловой поток. Третий способ требует использовать смешанные солверы вроде chtMultiRegionFoam, что усложняет саму задачу, для второго способа требуется использование groovyBC (т.к стандартную функцию patchAverage можно в таком случае использовать только для равномерного поля скоростей) В данном случае будем пользовать первым способом. Для этого напишем небольшую утилиту, которая будет рассчитывать распределение теплового потока и среднее значение, см. heatCalcTemp.tar.  Вся суть утилиты в следующем коде:

 
Сами кейсы при разных числах Рейнольдса в приложенных файлах Re10000.tar.gz Re20000.tar.gz Re50000.tar.gz
Отличия от турбулентного поперечного обтекания цилиндра заключается в следующем:
1) Появляются новые файлы:
constant/g – соответственно ускорение свободного падения, в нашем примере свободная конвекция роли не играет – поэтому отключена;
2) 0/T – температура;
0/kappat – турбулентная температуропроводность (в предыдущих версиях openFoam файл назывался alphat);
В constant/transportProperties необходимо указывать дополнительно следующие данные:

Значения beta и TRef необходимы для расчета силы Архимеда, которая учитывается в уравнениях Навье-Стокса как массовая, плотность же остается неизменной.
В папке system никаких пояснений не требуется.
Теперь сопоставление результатов.
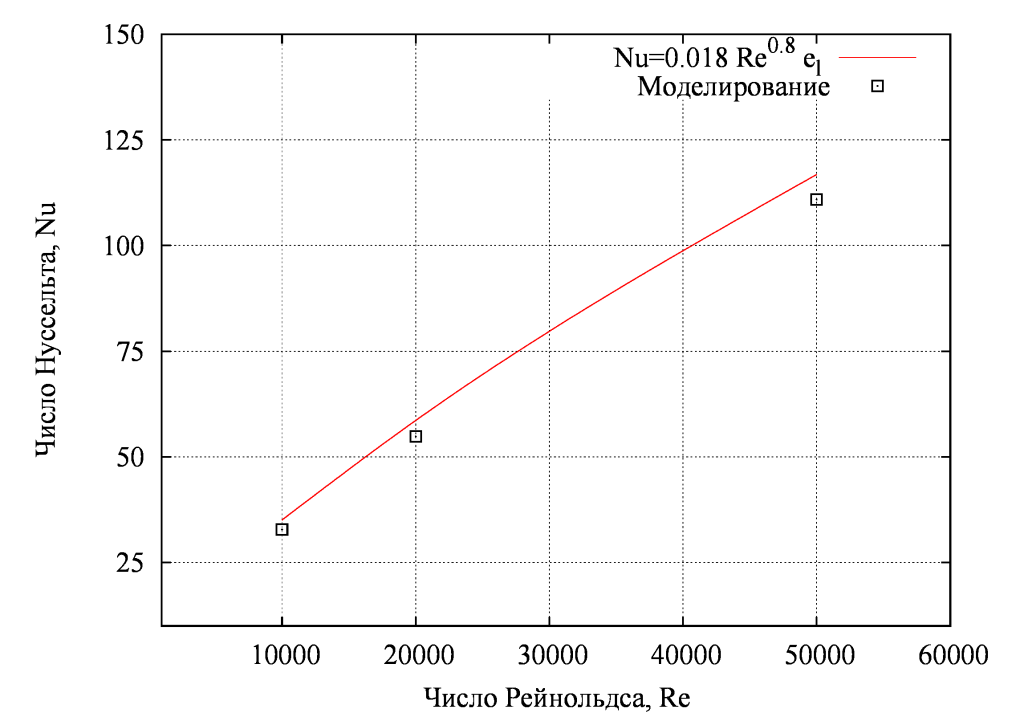
На рисунке ниже выполнено сопоставление расчетных данных с обобщающей зависимостью из справочника [2], максимальное расхождение 7%.

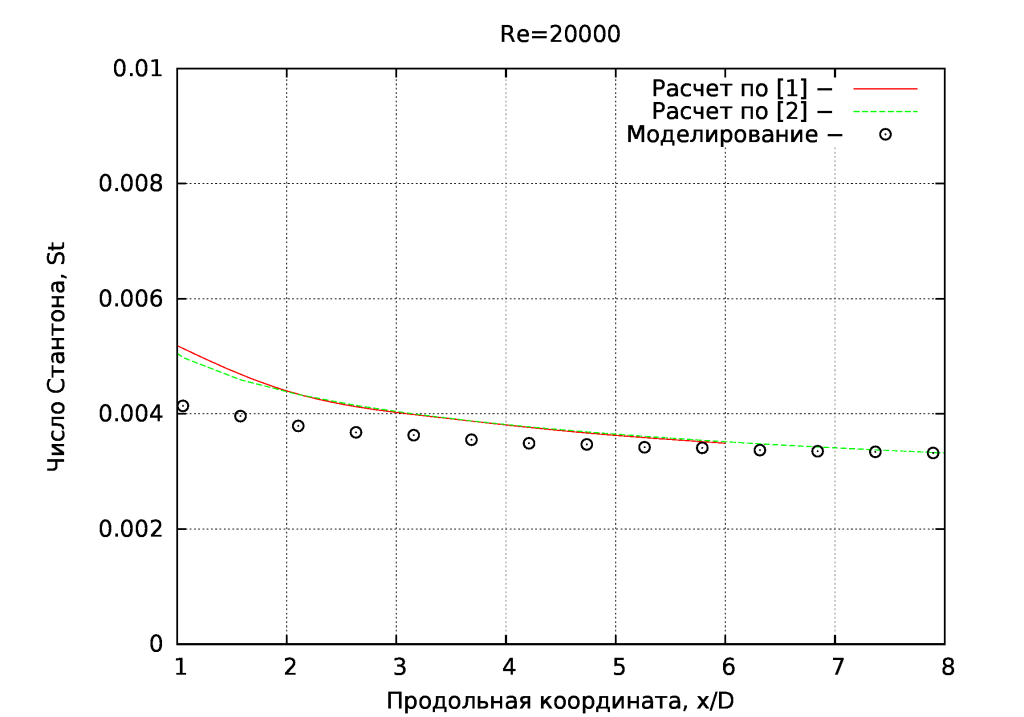
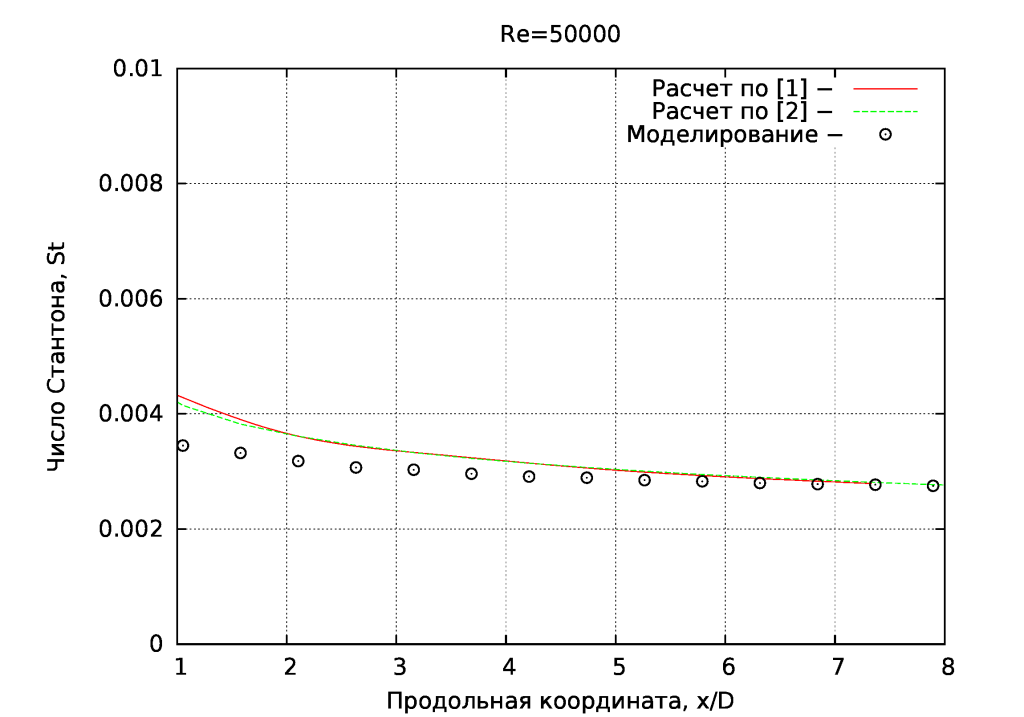
На рисунках ниже выполнено сопоставление распределения по длине коэффициента теплоотдачи (через число St), как с зависимостью для течения в трубе [1], так и вдоль неограниченной пластины [2].

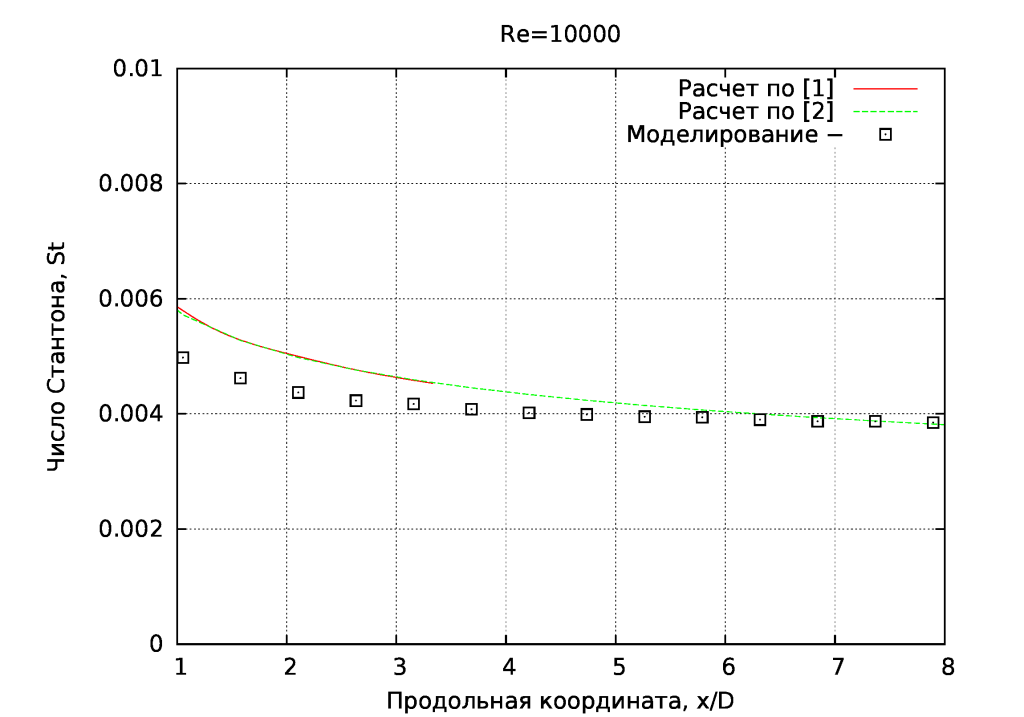
Как видно, на всех рисунках расчетные значения лежат ниже обобщающих эмперических завимостей, что связано с число , значение которого сильно влияет на интенсивность теплообмена. В нашем случае его можно было бы принять в пределах 0.7-0.8 для меньшего расхождения.

Литература:
1. Кутателадзе С.С. Тепломассообмен и трение в пограничном слое. 2-е изд.,
перераб. / С.С. Кутателадзе, А.И. Леонтьев. – М.: Энергоатомиздат, 1985. – 320 c.
2. Исаченко В.П. Телпопередача. 4-е изд., / В.П. Исаченко, В.А. Осипова, А.С. Сукомел – М.: Энергоатомиздат, 1981. – 416 с.