Моделирование теплопроводности. Пример 2

Проблемы примера №1 заключаются в следующем: 1) теплопроводность, теплоемкость и плотность материала зависят от температуры, 2) граничные условия 1-го рода редко встречаются на практике, чаще всего условия 3-го рода. В данном примере я покажу, как изменить стандартный солвер laplacianFoam для учета зависимости характеристик материала от температуры.
Решим задачу передачи теплоты теплопроводности через двухслойную бесконечную пластину толщиной 0,5 м, одна стенка которой нагрета до 800 С, вторая находится при 0 С. Первый слой толщиной 0,25 м с температуропроводностью 1.33e-7 м.кв/с и коэффициентом увеличения теплопроводности b=0.0025 1/С. Второй слой толщиной также 0,25 м, температуропроводность 6,67e-7 м.кв/с, b=0,0006 1/C. Получим установившийся режим и сравним с ручным аналитическим расчетом.

Сначала отредактируем исходный код laplacianFoam, см. приложенный файл myLaplacianFoam.tar.gz. Добавим в createFields.H скалярные поля DT (температуропроводность при температуре Tinf), b (коэффициент температурного увеличения теплопроводности):
$\lambda=\lambda _0 (1+b(T-T_{inf}))$
$a=a_0(1+b(T-T_{inf}))$

Info<< "Reading field DT\n" << endl;
volScalarField DT
(
   IOobject
   (
       "DT",
       runTime.timeName(),
       mesh,
       IOobject::MUST_READ,
       IOobject::AUTO_WRITE
   ),
   mesh
);

Info<< "Reading field b\n" << endl;
volScalarField b
(
   IOobject
   (
       "b",
       runTime.timeName(),
       mesh,
       IOobject::MUST_READ,
       IOobject::AUTO_WRITE
   ),
   mesh
);

Info<< "Reading field DT\n" << endl;

volScalarField DT

(

IOobject

(

"DT",

runTime.timeName(),

mesh,

IOobject::MUST_READ,

IOobject::AUTO_WRITE

mesh

);

Info<< "Reading field b\n" << endl;

volScalarField b

(

IOobject

(

"b",

runTime.timeName(),

mesh,

IOobject::MUST_READ,

IOobject::AUTO_WRITE

mesh

);

В данной работе изменением плотности и теплоемкости пренебрегаем, иначе нужно добавить еще коэффициентов:
$a=a_0 \frac {1+b(T-T_{inf}))} { (1+c(T-T_{inf}))(1+d(T-T_{inf}))}$ , где c и d аналогичные коэффициент для теплоемкости и плотности
В постоянных оставляем только температуру $T_{inf}$ , от которой начинается отсчет $a_0$ .

Info<< "Reading Tinf\n" << endl;
dimensionedScalar Tinf
(
    transportProperties.lookup("Tinf")
);

Info<< "Reading Tinf\n" << endl;

dimensionedScalar Tinf

(

transportProperties.lookup("Tinf")

);

Теперь дифференциальное уравнение имеет следующий вид:
$\frac {\partial T} {\partial \tau} = a_0(1+b(T_{inf}-T)) \nabla ^2 T$ .
Код, соответствующее данном ДУ:

solve
(
   fvm::ddt(T) - fvm::laplacian(DT*(1+b*(T-Tinf)), T)
);

solve

(

fvm::ddt(T) - fvm::laplacian(DT*(1+b*(T-Tinf)), T)

);

Отличия данной задачи от примера №1 в наличии файлов 0/b 0/DT, которые в принципе не требуют пояснений. См. приложенный файл varThermalConductivity.tar.gz

Задать распределение DT и b по длине пластины, чтобы сделать ее двухслойной, можно с помощью утилиты setFields, настройки для которой указываются в файле constant/setFieldsDict:

// значения по умолчанию
defaultFieldValues
(
        volScalarFieldValue DT 6.6667e-07
        volScalarFieldValue b  0.0006
);
// зоны с другими значениями
regions
(
    // выделяем зону параллелипипедом
    boxToCell
    {
        // задаем два угла
        box (0 -0.005 -0.005) (0.25 0.005 0.005);
        // ну и значения соответственно
        fieldValues
        (
                volScalarFieldValue DT 1.3333e-07
                volScalarFieldValue b 0.0025
        );
    }
);

// значения по умолчанию

defaultFieldValues

(

volScalarFieldValue DT 6.6667e-07

volScalarFieldValue b 0.0006

);

// зоны с другими значениями

regions

(

// выделяем зону параллелипипедом

boxToCell

{

// задаем два угла

box (0 -0.005 -0.005) (0.25 0.005 0.005);

// ну и значения соответственно

fieldValues

(

volScalarFieldValue DT 1.3333e-07

volScalarFieldValue b 0.0025

);

}

);

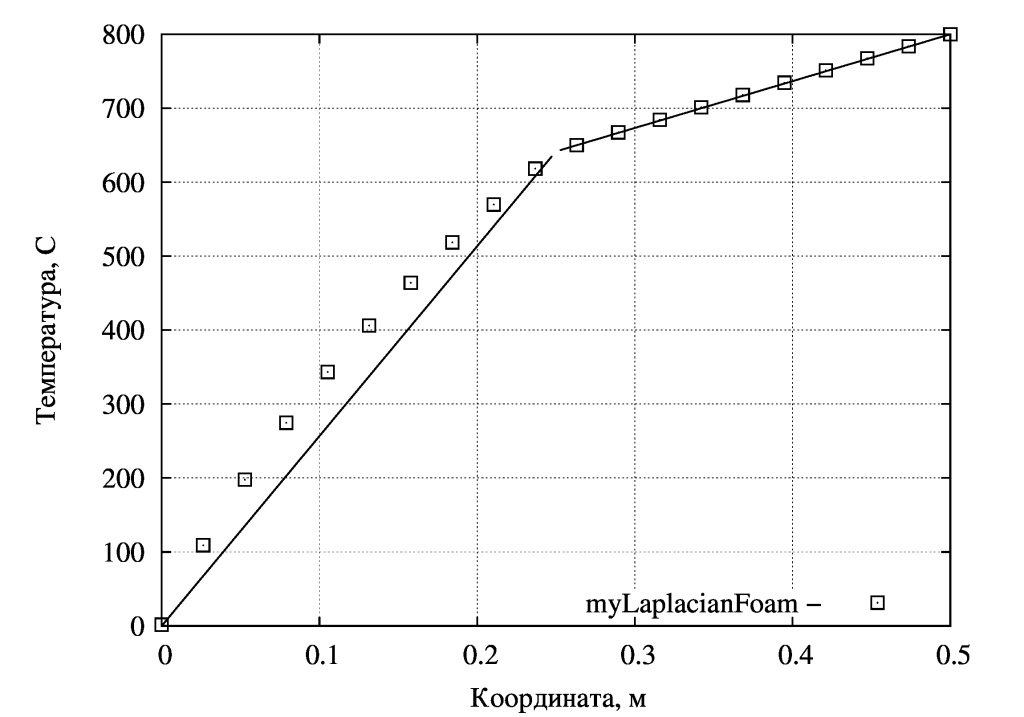
На рисунке ниже показано сопоставление профиля температуры полученных численным моделированием и аналитически. Т.к. на практике расчет производится по средней температуре слоя, то графики несколько расходятся. Нелинейность изменения температуры видна в диапазоне 0<x<0,25

Блог Загоскина А.А.

Аэродинамика, теплообмен, cfd, OpenFOAM

Моделирование теплопроводности. Пример 2