Продолжение, начало см:
Обтекание цилиндра. Re=1…30
Обтекание цилиндра. Re=100…200

Обтекание цилиндра в диапазоне Re>400 идет в турбулентном нестационарном режиме, все также образуется вихревая дорожка Кармана:

Основы моделирования турбулентности, модели турбулентности и области применимости наиболее удачно описаны в следующих книгах [1,2]. Вообще моделей турбулентности очень-очень много, но универсальной до сих пор нет, и видимо не появится. Наиболее распространенные на сегодня – модель Спаларта-Алмараса, и модель k-omega-SST Ментера, они обкатаны на большом спектре задач и их можно использовать “по умолчанию” в большинстве случаев. Модель k-epsilon уже очень старая, есть множество ее модификаций, в этой статье я буду использовать наиболее удачную модификацию Лаундера-Шармы, просто в качестве возможной альтернативы.
Есть мнение, что модель Спаларта-Алмараса нужно использовать в случае внешних задач, а модель k-omega-SST для внутренних, видимо так сложилось исторически, но я до сих пор не нашел этому подтверждение. При внешних задачах, несмотря на развитие пристенных функций, я всегда стараюсь использовать низкорейнольдсовые модели турбулентности и ближайшую ячейку располагать при y+<1, это всегда повышает точность, и потом не приходится мучаться поиском причин расхождения опыта и эксперимента.

См. приложенные файлы: kOmegaSST.tar.gz LaunderSharmaKE.tar.gz SA.tar.gz
Дополнительно к p,U надо указывать начальные условия, характеризующие турбулентность входящего потока: для SA – nuTilda, для kOmegaSST – k, omega, для LaunderSharmaKE – k, epsilon. Формулы для граничных условий nuTilda, k, omega, epsilon можно посмотреть здесь. Можно сделать двумя разными способами:
1) Принять, что течение происходит в канале, и соответственно интенсивность турбулентности можно определить через число Рейнольдса, а масштаб турбулентности через ширину канала;
2) Принять, что поток свободный (freestream) и задаваться отношением турбулентной и молекулярной вязкости nut/nu=0.1..0.2.
Файл 0/nut создавать не нужно, солвер его сам сгенерирует, где в основном будет условие “calculated”.
В constant/RASProperties указываем нужную модель турбулентности (SpalartAllmaras, kOmegaSST или LaunderSharmaKe):

и в constant/turbulenceProperties указываем, что будем использовать модель турбулентности

В system отличие от ламинарного режима будет в дополнительных строках fvSchemes:

.. и в fvSoluiton

Для моделей kOmegaSST и LSKE соответственно вместо div(phi,nuTilda) указываем div(phi,k)+div(phi,omega); div(phi,k)+div(epsilon) и в fvSolution меняем nuTilda на k+omega или k+epsilon
Шаг по времени для pisoFoam должен соответствовать числу Куранта Co=0.25…0.3, и строго меньше 1, иначе решение обвалится не успеешь глазом моргнуть.
В результате получаем схожие вихревые дорожки Кармана:
SA:

kOmegaSST:

LSKE:

А теперь самое непонятное, графики зависимостей Cd=f(Re) и St=f(Re):


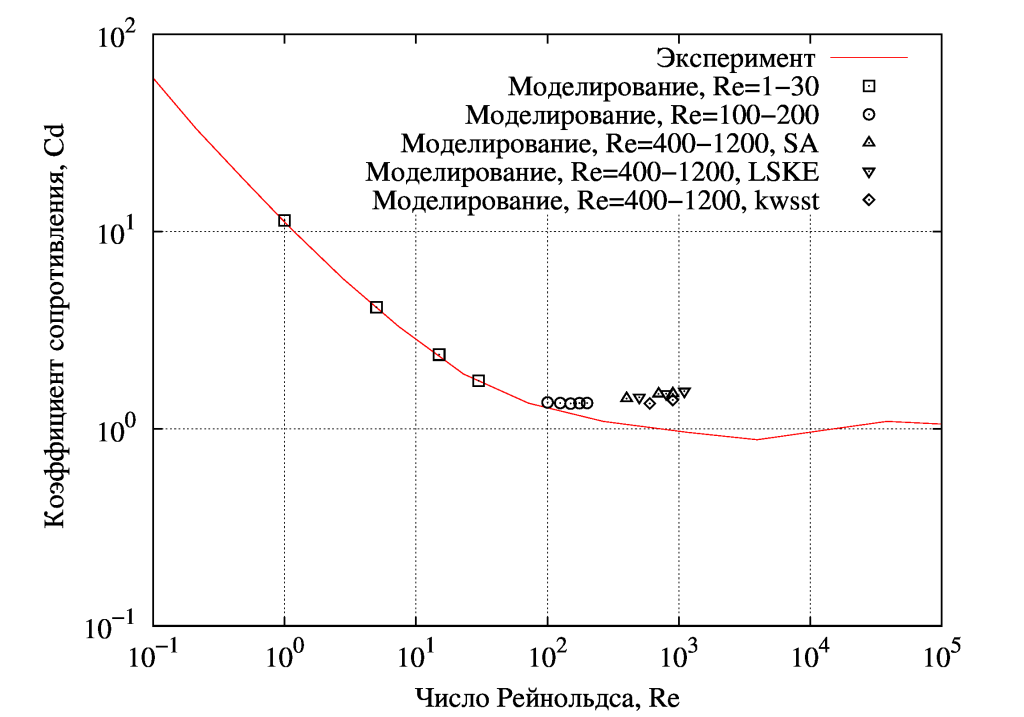
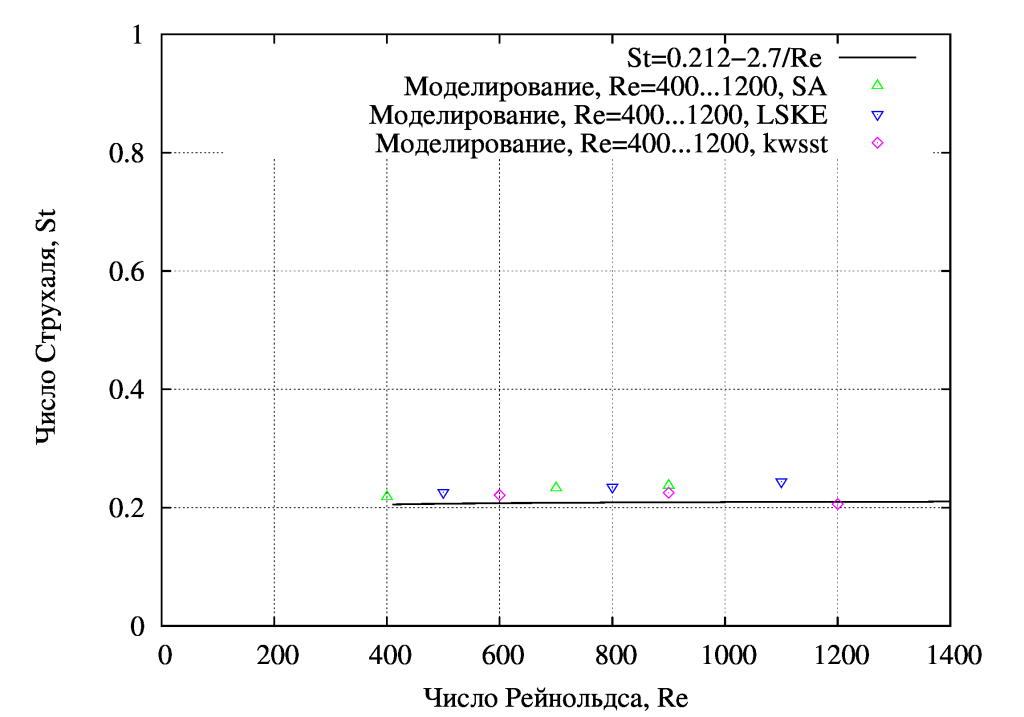
Видно, что все точки группируются вдоль какой-то общей линии, т.е. проблема явно не в выборе модели турбулентности. И проблема явно не в схемах дискретизации (везде самые точные – центральноразностные) и не в расчетной сетке. Можно предположить, что необходимо задавать другие граничные условия на входе для nuTilda, k, omega, epsilon, но если попытаться их увеличить, никакой вихревой дорожки не создается, да и задаю я их по общепринятым методикам. Скорее всего проблема заключается в непригодности RANS-моделей для отрывных течений, т.е. более точные результаты можно получить при помощи DES-методов.

Литература:
1. Белов, И.А. Моделирование турбулентных течений: Учебное пособие / И.А. Белов, С.А. Исаев. – СПб: Балт. гос. техн. ун-т., 2001. – 108 с.
2. Смирнов, Е.М. Конспект лекций дисциплины “Течения вязкой жидкости и модели турбулентности: методы расчета турбулентных течений” / Е.М. Смирнов, А.В. Гарбарук- 2010. – 127 с.