Проблемы примера №1 заключаются в следующем: 1) теплопроводность, теплоемкость и плотность материала зависят от температуры, 2) граничные условия 1-го рода редко встречаются на практике, чаще всего условия 3-го рода. В данном примере я покажу, как изменить стандартный солвер laplacianFoam для учета зависимости характеристик материала от температуры.
Решим задачу передачи теплоты теплопроводности через двухслойную бесконечную пластину толщиной 0,5 м, одна стенка которой нагрета до 800 С, вторая находится при 0 С. Первый слой толщиной 0,25 м с температуропроводностью 1.33e-7 м.кв/с и коэффициентом увеличения теплопроводности b=0.0025 1/С. Второй слой толщиной также 0,25 м, температуропроводность 6,67e-7 м.кв/с, b=0,0006 1/C. Получим установившийся режим и сравним с ручным аналитическим расчетом.
См. далее
Моделирование теплопроводности. Пример 1.
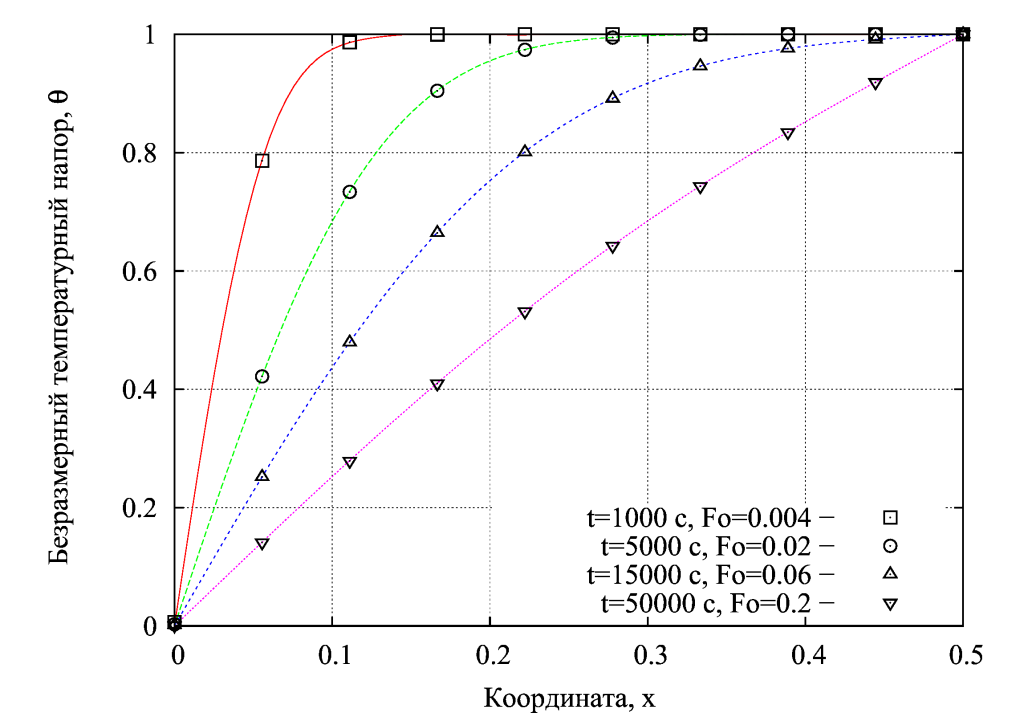
Моделирование нестационарной теплопроводности – наиболее простая задача теплообмена, решаемая с помощью численных методов. Особенно это просто сделать при простой геометрии, постоянной теплопроводности и граничных условиях первого рода. В разнообраных вычислительных платформах это делается при минимуме необходимых настроек и соответственно трудозатрат. В данной статье рассмотрен расчет в OpenFOAM охлаждения неограниченной пластины с температуропроводностью м.кв/с, толщиной 0,5 м, находящейся в начальный момент времени при t=500 c, если мгновенно уменьшить температуру одной стенки до t=0 С. Также выполнено сопоставление с аналитическим расчетом.
Дифференциальное уравнение распространения теплоты теплопроводностью при отсутствии внутренних источников достаточно простое [1]:
где – температура;
– время;
– температуропроводность;
– оператор Лапласа.
Код OpenFOAM в таком случае выглядит следующим образом [2]:
|
1 2 3 4 |
solve ( fvm::ddt(T) - fvm::laplacian(DT,T) ) |